题目内容
19.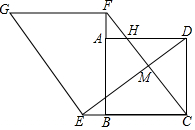 如图,在正方形ABCD中,点E,F分别是CB,BA延长线上的点,且BE=AF,连接DE,CF,CF交DE于点M,交AD于点H,过点E作EG⊥DE,使EG=DE,连接FG.
如图,在正方形ABCD中,点E,F分别是CB,BA延长线上的点,且BE=AF,连接DE,CF,CF交DE于点M,交AD于点H,过点E作EG⊥DE,使EG=DE,连接FG.(1)求证:四边形GECF是平行四边形;
(2)若FA=2,$\frac{AH}{AD}$=$\frac{1}{4}$,求EG的长.
分析 (1)证明△FBC≌△ECD,得到CF=BE,∠FCB=∠EDC,根据平行四边形的判定定理证明即可;
(2)根据相似三角形的性质列出比例式,计算即可.
解答 (1)证明:∵AB=BC,BE=AF,
∴BF=CE,
在△FBC和△ECD中,
$\left\{\begin{array}{l}{BC=CD}\\{∠FBC=∠ECD}\\{FB=EC}\end{array}\right.$,
∴△FBC≌△ECD,
∴CF=BE,∠FCB=∠EDC,
∵EG=ED,
∴CF=EG,
∵∠DEC+∠EDC=90°,
∴∠DEC+∠FCB=90°,
∴CF⊥DE,
∵EG⊥DE,
∴CF∥EG,
∴四边形GECF是平行四边形;
(2)解:∵$\frac{AH}{AD}$=$\frac{1}{4}$,
∴$\frac{AH}{DH}$=$\frac{1}{3}$,
∵△FAH∽△CDH,
∴$\frac{FA}{CD}$=$\frac{AH}{DH}$=$\frac{1}{3}$,
∵FA=2,
∴CD=6,
∴CE=BF=FA+AB=8,
∴EG=DE=$\sqrt{C{E}^{2}+C{D}^{2}}$=10.
点评 本题考查的是相似三角形的判定和性质、平行四边形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
9.将抛物线y=2x2向右平移1个单位,再向下平移2个单位后得到的抛物线的解析式为( )
| A. | y=2(x+1)2-2 | B. | y=2(x-1)2-2 | C. | y=2(x-2)2-1 | D. | y=2(x+2)2+1 |
4.下列关于点和线的说法中,正确的是( )
| A. | 线段比直线长 | |
| B. | 过同一平面内的两点,可以作三条直线 | |
| C. | 一条射线有两个端点 | |
| D. | 两点之间的所有连线中,线段最短 |