题目内容
已知：如图，△ABC和△ADE都是等边三角形．求证：∠ACD=∠ABE．考点：全等三角形的判定与性质
专题：证明题
分析：首先根据等边三角形的性质可得AE=AD，AC=AB，∠EAD=∠CAB=60°，然后再证明△ACD≌△ABE，根据全等三角形对应角相等可得结论．
解答：证明：∵△ABC和△ADE都是等边三角形，
∴AE=AD，AC=AB，∠EAD=∠CAB=60°，
在△ACD和△ABE中
，
∴△ACD≌△ABE（SAS），
∴∠ACD=∠ABE．
∴AE=AD，AC=AB，∠EAD=∠CAB=60°，
在△ACD和△ABE中
|
∴△ACD≌△ABE（SAS），
∴∠ACD=∠ABE．
点评：此题主要考查了全等三角形的判定和性质，全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，直线y=
如图，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上．将线段AB绕点B顺时针旋转90°，得线段A′B，点A的对应点为A′，连接AA′交线段BC于点D．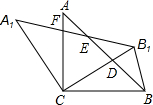
如图，在△ABC中，AC=BC，∠ACB=90°，将△ABC绕点C逆时针旋转α角（0°＜α＜90°），得到△A1B1C，连接BB1，设CB1交AB于D，A1B1分别交AB，AC于E，F
如图，二次函数y=ax2+bx的图象经过原点，顶点的纵坐标为2，若一元二次方程ax2+bx+k=0有实数根，则k的取值范围是（ ）
| A、k≤-2 | B、k≥2 |
| C、k≤2 | D、k≥-2 |
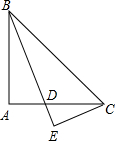已知：△ABC是等腰直角三角形，∠A=90°，BD平分∠ABC交AC于点D，CE⊥BD．
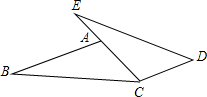如图，E、A、C三点共线，AB∥CD，∠B=∠E，AC=CD，求证：BC=ED．