题目内容
若一个正多边形的一个外角为60°，则它的内切圆半径与外接圆半径之比是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：正多边形和圆
专题：
分析：由一个正多边形的一个外角为60°，可得是正六边形，然后从内切圆的圆心和外接圆的圆心向三角形的三边引垂线，构建直角三角形，解三角形即可．
解答：解：∵一个正多边形的一个外角为60°，
∴360°÷60°=6，
∴这个正多边形是正六边形，
设这个正六边形的半径是r，
则外接圆的半径r，
∴内切圆的半径是正六边形的边心距，即是
r，
∴它的内切圆半径与外接圆半径之比是：
：2．
故选A．
∴360°÷60°=6，
∴这个正多边形是正六边形，
设这个正六边形的半径是r，
则外接圆的半径r，
∴内切圆的半径是正六边形的边心距，即是
| ||
| 2 |
∴它的内切圆半径与外接圆半径之比是：
| 3 |
故选A．
点评：考查了正多边形和圆，正多边形的计算一般是通过中心作边的垂线，连接半径，把正多边形中的半径，边长，边心距，中心角之间的计算转化为解直角三角形．
练习册系列答案
一本好题口算题卡系列答案
相关题目
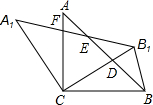如图，在△ABC中，AC=BC，∠ACB=90°，将△ABC绕点C逆时针旋转α角（0°＜α＜90°），得到△A1B1C，连接BB1，设CB1交AB于D，A1B1分别交AB，AC于E，F
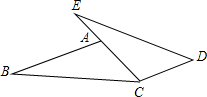如图，E、A、C三点共线，AB∥CD，∠B=∠E，AC=CD，求证：BC=ED．
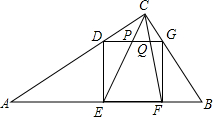如图，△ABC中，∠C=90°，AC=4，BC=3，正方形DEFG的四个顶点分别在边AC、AB、CB上．
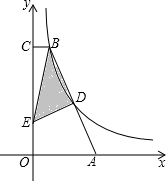如图，B、D两点均在双曲线y=
如图是一个正方体的表面展开图，如果正方体相对的面上标注的值相等，那么x+2y=