题目内容
1.已知关于x的二次函数y1=a(x-x1)(x-x2)与函数y2=a(x-x1)(x-x2)+k(x-x1),其中a,k,x1,x2是常数,a≠0,k≠0,x1≠x2.若当y2=0时,只有一个自变量x的值与其对应,则下列结论成立的是( )| A. | $\frac{k}{a}$=x1-x2 | B. | $\frac{k}{a}$=x2-x1 | C. | $\frac{k}{a}$=x1+x2 | D. | $\frac{k}{a}$=-(x1+x2) |
分析 由当y2=0时,只有一个自变量x的值与其对应,可得出函数y2=a(x-x1)(x-x2)+k(x-x1)的图象与x轴只有一个交点,将y2=a(x-x1)(x-x2)+k(x-x1)变形为两点式,即可得出$\frac{k}{a}$=x2-x1,此题得解.
解答 解:∵当y2=0时,只有一个自变量x的值与其对应,
∴函数y2=a(x-x1)(x-x2)+k(x-x1)的图象与x轴只有一个交点,
∴y2=a(x-x1)(x-x2)+k(x-x1)=(x-x1)[a(x-x2)+k]=a(x-x1)(x-x2+$\frac{k}{a}$),
∴x2-$\frac{k}{a}$=x1,
∴$\frac{k}{a}$=x2-x1.
故选B.
点评 本题考查了二次函数的性质、抛物线与x轴的交点问题以及二次函数的三种形式,由当y2=0时,只有一个自变量x的值与其对应,找出函数y2=a(x-x1)(x-x2)+k(x-x1)的图象与x轴只有一个交点是解题的关键.

练习册系列答案
相关题目
1.在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外完全相同,其中有5个黄球,4个蓝球.若随机摸出一个蓝球的概率为$\frac{1}{3}$,则随机摸出一个红球的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{12}$ | D. | $\frac{1}{2}$ |
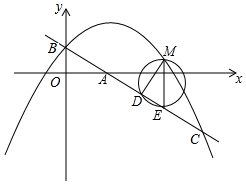 在平面直角坐标系中,直线y=-$\frac{3}{4}$x+1交y轴于点B,交x轴于点A,抛物线y=-$\frac{1}{2}$x2+bx+c经过点B,与直线y=-$\frac{3}{4}$x+1交于点C(4,-2).
在平面直角坐标系中,直线y=-$\frac{3}{4}$x+1交y轴于点B,交x轴于点A,抛物线y=-$\frac{1}{2}$x2+bx+c经过点B,与直线y=-$\frac{3}{4}$x+1交于点C(4,-2). 如图,有一正方体的房间,在房间内的一角A处由一只蚂蚁,它想到房间的另一角B处去吃食物,请问它采取怎样的行走路线是最近的?如果一只蜜蜂,要从A到B怎样飞是最近的?请你画图展示.
如图,有一正方体的房间,在房间内的一角A处由一只蚂蚁,它想到房间的另一角B处去吃食物,请问它采取怎样的行走路线是最近的?如果一只蜜蜂,要从A到B怎样飞是最近的?请你画图展示.
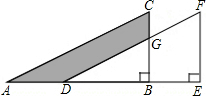 如图,将直角三角形ABC沿AB方向平移AD长的距离得到直角三角形DEF,已知BE=5,EF=8,CG=3.则图中阴影部分面积$\frac{65}{2}$.
如图,将直角三角形ABC沿AB方向平移AD长的距离得到直角三角形DEF,已知BE=5,EF=8,CG=3.则图中阴影部分面积$\frac{65}{2}$.