题目内容
18．计算|1-$\sqrt{3}}$|+（$\frac{{\sqrt{5}}}{2}}$）0=$\sqrt{3}$．分析 先利用零指数幂的意义计算，然后去绝对值后合并．
解答 解：原式=$\sqrt{3}$-1+1
=$\sqrt{3}$．
故答案为$\sqrt{3}$．
点评 本题考查了实数的运算：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到有的顺序进行．
练习册系列答案
相关题目
8．已知函数y=$\sqrt{a-2}$x${\;}^{{a}^{2}-8}$+3是一次函数，则a的值是（ ）
| A． | a=±3 | B． | a=3 | C． | a=-3 | D． | a=1 |
13．计算（ab2）3的结果是（ ）
| A． | 3ab2 | B． | ab6 | C． | a3b5 | D． | a3b6 |
3．
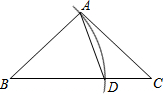如图，在△ABC中，以点B为圆心，以BA长为半径画弧交边BC于点D，连接AD．若∠B=40°，∠C=36°，则∠DAC的度数是（ ）
如图，在△ABC中，以点B为圆心，以BA长为半径画弧交边BC于点D，连接AD．若∠B=40°，∠C=36°，则∠DAC的度数是（ ）| A． | 70° | B． | 44° | C． | 34° | D． | 24° |
1．已知关于x的二次函数y1=a（x-x1）（x-x2）与函数y2=a（x-x1）（x-x2）+k（x-x1），其中a，k，x1，x2是常数，a≠0，k≠0，x1≠x2．若当y2=0时，只有一个自变量x的值与其对应，则下列结论成立的是（ ）
| A． | $\frac{k}{a}$=x1-x2 | B． | $\frac{k}{a}$=x2-x1 | C． | $\frac{k}{a}$=x1+x2 | D． | $\frac{k}{a}$=-（x1+x2） |
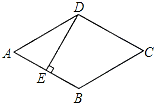如图，菱形ABCD的边长是2cm，E是AB的中点，且DE⊥AB，则对角线AC的长为2$\sqrt{3}$cm．