题目内容
19.一块长40m、宽20m的长方形操场,现要将它的面积增加一倍,但不改变操场的形状,问长和宽应增加多少?设它的宽增加xm,根据题意可以列方程:(20+x)•(40+2x)=2×40×20.分析 设它的宽增加xm,则长增加2xm,根据面积增加一倍,列方程即可.
解答 解:设它的宽增加xm,则长增加2xm,
由题意得,(20+x)•(40+2x)=2×40×20.
故答案为:(20+x)•(40+2x)=2×40×20.
点评 本题考查了由实际问题抽象出一元二次方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程.

练习册系列答案
相关题目
10.小强买了张50元的乘车IC卡,如果他乘车的次数用m表示,则记录他每次乘车后的余额n(元)如下表:
(1)写出乘车的次数m表示余额n的关系式.
(2)利用上述关系式计算小强乘了10次车还剩下多少元?
(3)小强最多能乘几次车?
| 次数 m | 余额 n(元) |
| 1 | 50-0.9 |
| 2 | 50-1.8 |
| 3 | 50-2.7 |
| 4 | 50-3.6 |
| … | … |
(2)利用上述关系式计算小强乘了10次车还剩下多少元?
(3)小强最多能乘几次车?
7.把下列图形:①线段,②直角三角形,③锐角,④平行四边形,⑤长方形,沿着某条直线对折,这条直线两旁的部分能够完全重合的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.一个多边形截去一个角后,形成的新多边形的内角和其其外角和的2倍,那么原多边形的边数为( )
| A. | 5 | B. | 5或6 | C. | 4或5或6 | D. | 5或6或7 |
9.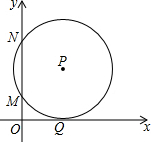 如图,在平面直角坐标系中,点在第一象限,⊙P与x轴相切于点Q,与y轴交于M(2,0),N(0,8)两点,则点P的坐标是( )
如图,在平面直角坐标系中,点在第一象限,⊙P与x轴相切于点Q,与y轴交于M(2,0),N(0,8)两点,则点P的坐标是( )
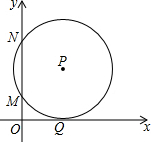 如图,在平面直角坐标系中,点在第一象限,⊙P与x轴相切于点Q,与y轴交于M(2,0),N(0,8)两点,则点P的坐标是( )
如图,在平面直角坐标系中,点在第一象限,⊙P与x轴相切于点Q,与y轴交于M(2,0),N(0,8)两点,则点P的坐标是( )| A. | (5,3) | B. | (3,5) | C. | (5,4) | D. | (4,5) |
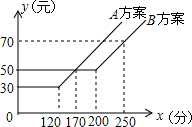 某移动通讯公司提供的A、B两种方案通讯费用y(元)与通话时间x(分)之间的关系如图所示.以下说法:
某移动通讯公司提供的A、B两种方案通讯费用y(元)与通话时间x(分)之间的关系如图所示.以下说法: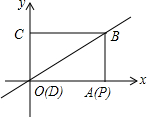 如图,矩形ABCD的两条边在坐标上,点D与原点重合,对角线BD所在直线的函数关系式为y=$\frac{3}{4}$x,AD=8,点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C用了14S.
如图,矩形ABCD的两条边在坐标上,点D与原点重合,对角线BD所在直线的函数关系式为y=$\frac{3}{4}$x,AD=8,点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C用了14S.