题目内容
8.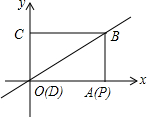 如图,矩形ABCD的两条边在坐标上,点D与原点重合,对角线BD所在直线的函数关系式为y=$\frac{3}{4}$x,AD=8,点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C用了14S.
如图,矩形ABCD的两条边在坐标上,点D与原点重合,对角线BD所在直线的函数关系式为y=$\frac{3}{4}$x,AD=8,点P从点A出发做匀速运动,沿矩形ABCD的边经过点B到达点C用了14S.(1)求矩形ABCD的周长;
(2)若矩形ABCD绕点D按逆时旋转90°后,这时在点P运动的同时,矩形ABCD沿OB方向以每秒1个单位长度运动,求运动到第5S时,点P的坐标;
(3)在(2)条件下,设矩形运动的时间为t,当0≤t≤6时,点P所经过的路线是一条线段,求线段所在直线的函数关系式?
分析 (1)在函数关系式为y=$\frac{3}{4}$x中求得当x=8时函数值,即可求得B的坐标,则矩形ABCD的周长即可求得;
(2)首先求得点D沿直线y=$\frac{3}{4}$x运动5s后的坐标,根据矩形ABCD的边长以及P运动的距离即可求得P的坐标;
(3)点P运动前的位置为(0,8),根据(2)得到的5秒后P的坐标,利用待定系数法即可求得.
解答 解:(1)∵AD=8,点B在上y=$\frac{3}{4}$x,则y=6;
∴点B坐标为(8,6),AB=6,矩形的周长为28.
(2)由(1)知,AB+BC=14,点P走过AB、BC的时间为14s,
因此,点P的速度为每秒1个单位.矩形旋转前,点B坐标为(8,6),
这时DB的函数关系式为y=$\frac{3}{4}$x,矩形沿OB方向以每秒1个单位长度运动,出发5s后,OD=5,
此时点D坐标为(-3,4),
同时P沿AB方向运动5个单位长度,则点P坐标为(-8,12),
(3)点P运动前的位置为(0,8),5秒后运动到(-8,12),已知它运动路线是一条线段,设线段所在直线为y=kx+b.
则$\left\{\begin{array}{l}{b=8}\\{-8k+b=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=8}\end{array}\right.$,
∴所求函数的解析式是y=-$\frac{1}{2}$x+8.
点评 本题考查了图形的旋转以及待定系数法求函数解析式,正确求得旋转后P的坐标是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
18.下列说法正确的是( )
| A. | a的倒数是$\frac{1}{a}$ | B. | 任何有理数都有倒数 | ||
| C. | -$\frac{1}{4}$的倒数是-4 | D. | $\frac{1}{2}$的倒数是-2 |
16.下列命题中,逆命题为真命题的是( )
| A. | 四边形是多边形 | B. | 两直线平行,同旁内角互补 | ||
| C. | 如果a=0,b=0,那么ab=0 | D. | 相等的两个数平方一定相等 |
13.使代数式$\sqrt{x+2}$-$\sqrt{1-2x}$有意义的x的取值范围是( )
| A. | x≥-2 | B. | x≤$\frac{1}{2}$ | C. | -2$≤x≤\frac{1}{2}$ | D. | 一切实数 |