题目内容
9.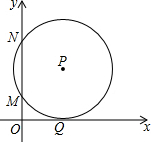 如图,在平面直角坐标系中,点在第一象限,⊙P与x轴相切于点Q,与y轴交于M(2,0),N(0,8)两点,则点P的坐标是( )
如图,在平面直角坐标系中,点在第一象限,⊙P与x轴相切于点Q,与y轴交于M(2,0),N(0,8)两点,则点P的坐标是( )| A. | (5,3) | B. | (3,5) | C. | (5,4) | D. | (4,5) |
分析 作PH⊥MN于H,连结PQ,PM,易得MN=6,根据垂径定理得HM=HN=$\frac{1}{2}$MN=3,则OH=OM+MH=5,再根据切线的性质得PQ⊥x轴,于是可判断四边形OQPH为矩形,所以PQ=OH=5,然后在Rt△PMH中利用勾股定理计算出PH=4,从而可得到P点坐标.
解答 解:作PH⊥MN于H,连结PQ,PM,
∵M(2,0),N(0,8),
∴OM=2,ON=8,
∴MN=6,
∵PH⊥MN,
∴HM=HN=$\frac{1}{2}$MN=3,
∴OH=OM+MH=2+3=5,
∵⊙P与x轴相切于点Q,
∴PQ⊥x轴,
∴四边形OQPH为矩形,
∴PQ=OH=5,
∴PM=PQ=5,
在Rt△PMH中,PH=$\sqrt{P{M}^{2}-H{M}^{2}}$=4,
∴P(4,5).
故选D.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了坐标与图形性质.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
14.当二次三项式4x2+kx+25是完全平方式时,k的值是( )
| A. | 20 | B. | 10 | C. | -20 | D. | 绝对值是20的数 |
19.上周五某股民以每股20元的价格买进某种股票,如表为本周内该股票的涨跌情况:
如果在本周五收盘时,该股民将这种股票卖出,那么每股的售出价格是20.15元.
| 星 期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +0.20 | +0.15 | -0.10 | -0.30 | +0.20 |