题目内容
已知E、F两点把线段AB分成2:3:4三部分,D是线段AB的中点,FB=12,求DF的长及AE:ED.
考点:两点间的距离
专题:
分析:根据E、F两点把线段AB分成2:3:4三部分,可得AE、EF、FB的长,根据线段和差,可得AB的长,根据线段中点的性质,可得AD、BD的长,根据线段的和差,可得DF、ED的长,根据比的意义,可得答案.
解答:解:如图: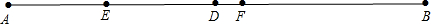 ,
,
由AE:EF:FB=2:3:4,BF=12,得
AE=2×3=6,EF=3×3=9.
由线段的和差,得
AB=AE+EF+FB=6+9+12=27.
由D是AB的中点,得
AD=BD=
AB=
.
由线段的和差,得
DF=DB-BF=
-12=
;
ED=AD-AE=
-6=
,
AE:ED=6:
=4:5.
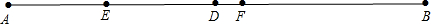 ,
,由AE:EF:FB=2:3:4,BF=12,得
AE=2×3=6,EF=3×3=9.
由线段的和差,得
AB=AE+EF+FB=6+9+12=27.
由D是AB的中点,得
AD=BD=
| 1 |
| 2 |
| 27 |
| 2 |
由线段的和差,得
DF=DB-BF=
| 27 |
| 2 |
| 3 |
| 2 |
ED=AD-AE=
| 27 |
| 2 |
| 15 |
| 2 |
AE:ED=6:
| 15 |
| 2 |
点评:本题考查了两点间的距离,利用E、F两点把线段AB分成2:3:4三部分,得出AE、EF的长是解题关键,又利用了线段的和差,线段中点的性质.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
 如图,有两个相似的星星图案,则x的值为( )
如图,有两个相似的星星图案,则x的值为( )| A、8 | B、10 | C、12 | D、15 |
 求阴影部分的面积.(取π=3)
求阴影部分的面积.(取π=3) 如图,已知线段AC,点D为AC的中点,BC=
如图,已知线段AC,点D为AC的中点,BC= 如图,四边形ABCD中,∠C=75°,∠D=120°,cosB=
如图,四边形ABCD中,∠C=75°,∠D=120°,cosB=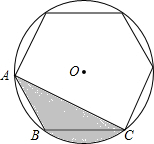 如图,在半径为6cm的圆内画一个正六边形,求阴影部分的面积.
如图,在半径为6cm的圆内画一个正六边形,求阴影部分的面积.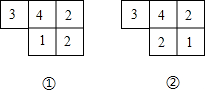 如图都是由几个小正方体所搭成的几何体的俯视图,小正方体中的数字表示在该位置的小正方体的个数.
如图都是由几个小正方体所搭成的几何体的俯视图,小正方体中的数字表示在该位置的小正方体的个数.