题目内容
14．先化简代数式：（$\frac{3x}{x-2}$-$\frac{x}{x+2}$）•$\frac{{x}^{2}-4}{x}$，再选择一个你认为合适的x值计算求值．分析 原式括号中两项通分并利用同分母分式的减法法则计算，约分得到最简结果，把x=1代入计算即可求出值．
解答 解：原式=$\frac{3x（x+2）-x（x-2）}{（x+2）（x-2）}$•$\frac{（x+2）（x-2）}{x}$=3（x+2）-（x-2）=3x+6-x+2=2x+8，
当x=1时，原式=2+8=10（注意x取值不能取0、2、-2）．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC中，AD平分∠BAC，过点D分别作DE∥AC、DF∥AB，分别交AB、AC于点E、F．求证：四边形AEDF是菱形．
如图，l1∥l2∥l3，则∠1，∠2，∠3之间的数量关系是∠1+∠3-∠2=180°．
19．下列计算中，正确的是（ ）
| A． | （2x+1）（2x-1）=2x2-1 | B． | （x-4）2=x2-16 | ||
| C． | （x+5）（x-6）=x2-x-30 | D． | （x+2y）2=x2+2xy+4y2 |
6．
如图，Rt△ABC中，∠B=90°，AB=6，BC=9，将△ABC折叠，使C点与AB的中点D重合，折痕为EF，则线段BF的长为（ ）
如图，Rt△ABC中，∠B=90°，AB=6，BC=9，将△ABC折叠，使C点与AB的中点D重合，折痕为EF，则线段BF的长为（ ）| A． | $\frac{5}{2}$ | B． | $\frac{9}{2}$ | C． | 4 | D． | 5 |
3．
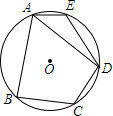如图，在⊙O的内接四边形ABCD中，AB=AD，∠C=120°，点E在弧AD上．若AE恰好为⊙O的内接正十边形的一边，弧DE的度数为（ ）
如图，在⊙O的内接四边形ABCD中，AB=AD，∠C=120°，点E在弧AD上．若AE恰好为⊙O的内接正十边形的一边，弧DE的度数为（ ）| A． | 75° | B． | 80° | C． | 84° | D． | 90° |
4．下列运算正确的是（ ）
| A． | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B． | $\sqrt{4\frac{1}{9}}=2\frac{1}{3}$ | C． | $\sqrt{8}-\sqrt{2}=\sqrt{2}$ | D． | $\sqrt{8}÷\sqrt{2}=4$ |