题目内容
16.解方程:(1)$\frac{3}{x+2}=\frac{2}{x-1}$
(2)$\frac{x+1}{x-1}-\frac{4}{{{x^2}-1}}=1$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)两边同时乘以(x+2)(x-1)得:3(x-1)=2(x+2),
解得:x=7,
检验:当x=7时,(x+2)(x-1)≠0,
∴x=7是原方程的解;
(2)两边同时乘以(x+1)(x-1)得(x+1)2-4=(x+1)(x-1),
解得:x=1,
检验:当x=1时,(x+1)(x-1)=0,
∴x=1是原方程的增根,
∴原方程无解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程时注意要检验.

练习册系列答案
相关题目
6.下列结论错误的是( )
| A. | 垂直于同一直线的两条直线互相平行 | |
| B. | 两直线平行,同旁内角互补 | |
| C. | 过直线外一点有且只有一条直线与这条直线平行 | |
| D. | 同一平面内,不相交的两条直线叫做平行线 |
5.下列命题是真命题的是( )
| A. | 如果两个角不相等,那么这两个角不是对顶角 | |
| B. | 两个互补的角一定是邻补角 | |
| C. | 如果两个角是同位角,那么这两个角一定相等 | |
| D. | 如果a2=b2,那么a=b |
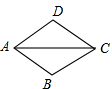 如图,四边形ABCD是菱形,∠ACD=30°,AB=6.
如图,四边形ABCD是菱形,∠ACD=30°,AB=6.