题目内容
8.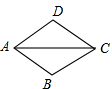 如图,四边形ABCD是菱形,∠ACD=30°,AB=6.
如图,四边形ABCD是菱形,∠ACD=30°,AB=6.(1)求∠ABC的度数;
(2)求AC的长.
分析 (1)由四边形ABCD是菱形,∠ACD=30°,可求得∠BCD的度数,继而求得答案;
(2)首先连接BD交AC于点O,则∠AOB=90°,AO=CO,然后由含30°的直角三角形的性质,求得OB的长,再利用勾股定理的知识求得OA的长,继而求得答案.
解答 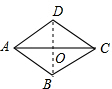 解:(1)∵四边形ABCD是菱形,∠ACD=30°,
解:(1)∵四边形ABCD是菱形,∠ACD=30°,
∴∠BCD=2∠ACD=60°,
∴∠ABC=180°-60°=120°;
(2)连接BD交AC于点O,则∠AOB=90°,AO=CO,
又∵∠ACD=∠BAC=30°,
∴在Rt△AOB中,OB=$\frac{1}{2}$AB=3,
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴AC=6$\sqrt{3}$.
点评 此题考查了利用菱形的性质、勾股定理以及含30°的直角三角形的性质.注意掌握辅助线的作法是解此题的关键.

练习册系列答案
相关题目
18.把$\sqrt{1.5}$化成最简二次根式为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
13.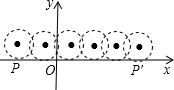 如图,半径为1个单位长度的圆从点P(-2,0)沿x轴向右滚动一周,圆上的一点由P点到达P′点,则点P′的横坐标是( )
如图,半径为1个单位长度的圆从点P(-2,0)沿x轴向右滚动一周,圆上的一点由P点到达P′点,则点P′的横坐标是( )
 如图,半径为1个单位长度的圆从点P(-2,0)沿x轴向右滚动一周,圆上的一点由P点到达P′点,则点P′的横坐标是( )
如图,半径为1个单位长度的圆从点P(-2,0)沿x轴向右滚动一周,圆上的一点由P点到达P′点,则点P′的横坐标是( )| A. | 4 | B. | 2π | C. | π-2 | D. | 2π-2 |
17.以下列长度为三角形边长,不能构成直角三角形的是( )
| A. | 5,12,13 | B. | 4,5,6 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 7,24,25 |
18.计算$\sqrt{4}$的结果是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±4 |
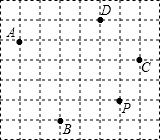 如图,已知点P($\frac{1}{2}$x+1,3x-8)的横、纵坐标恰好为某个正数的两个平方根.
如图,已知点P($\frac{1}{2}$x+1,3x-8)的横、纵坐标恰好为某个正数的两个平方根.