题目内容
7.解下列不等式(组),并把解集在数轴上表示出来.(1)$\frac{x-1}{3}$≤5-x
(2)$\left\{\begin{array}{l}{3x+1>4}\\{4-2x≥0}\end{array}\right.$.
分析 (1)去分母,去括号,移项,合并同类项,系数化成1,最后在数轴上表示出来即可.
(2)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:(1)$\frac{x-1}{3}$≤5-x
x-1≤15-3x,
x+3x≤15+1,
4x≤16,
解得x≤4,
在数轴上表示不等式的解集为: .
.
(2)$\left\{\begin{array}{l}{3x+1>4①}\\{4-2x≥0②}\end{array}\right.$
由①得,x>1;
由②得,x≤2;
所以不等式的解集为1<x≤2,
在数轴上表示为: .
.
点评 本题考查了解一元一次不等式(组),在数轴上表示不等式(组)的解集的应用,能根据不等式的性质求出不等式的解集是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.把$\sqrt{1.5}$化成最简二次根式为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
15.下列式子可以用平方差公式计算的是( )
| A. | (x-4)(4-x) | B. | (-a-3)(3-a) | C. | (a+b)(-a-b) | D. | (2y-4)(-4+2y) |
17.以下列长度为三角形边长,不能构成直角三角形的是( )
| A. | 5,12,13 | B. | 4,5,6 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 7,24,25 |
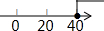
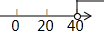


 如图,将Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,使AB′恰好经过点C,连接BB′,则∠BAC′的度数为80°.
如图,将Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,使AB′恰好经过点C,连接BB′,则∠BAC′的度数为80°.