题目内容
8.某商店经销甲、乙两种商品,现有如下信息:信息1:甲乙两种商品的进货单价之和是10元.
信息2:甲商品零售单价比进货单价多2元,乙商品零售单价比进货单价的2倍少3元.
信息3:按零售单价购买甲商品2件和乙商品3件,共付了31元.
请根据以上信息,解答下列问题:
(1)求甲、乙两种商品的进货单价各是多少元;
(2)该商店平均每天卖出甲商品500件,乙商品200件.经调查发现,甲、乙两种商品零售单价分别每涨0.5元,这两种商品每天各少销售50件,为了使每天获取更大的利润,商店决定把甲乙两种商品的零售价都涨n元,在不考虑其他因素的条件下,当甲、乙两种商品的零售单价分别为多少元时,才能使商店每天销售这两种商品获取的利润最大?每天的最大利润是多少元?
分析 (1)根据图上信息可以得出甲乙商品之间价格之间的等量关系,即可得出方程组求出即可;
(2)把商店的销售利润表示成n的函数,根据函数的性质即可求解.
解答 解:(1)假设甲、乙两种商品的进货单价各为x,y元,则甲的零售价是(x+2)元,乙的零售价是(2y-3)元.
根据题意得:
$\left\{\begin{array}{l}{x+y=10}\\{2(x+2)+3(2y-3)=31}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=6}\\{y=4}\end{array}\right.$,
∴甲、乙零售单价分别为6元和4元;
(2)甲、乙两种商品的零售单价都涨n元,则甲、乙商品的销售量分别是(500-100n)、(200-100n)件,甲的每件利润是(2+n)元,乙每件的利润是2y-3-y+n=y-3+n=1+n元.
则商店的每天的销售利润w=(500-100n)(2+n)+(200-100n)(1+n),即w=-200n2+400n+1200,
则当n=-$\frac{400}{2×(-200)}$=1时,w最大,最大值是:1400元.
点评 此题主要考查了一元二次方程的应用,此题比较典型也是近几年中考中热点题型,注意表示总利润时表示出商品的单件利润和所卖商品件数是解决问题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
18.某校数学竞赛和演讲比赛中,七年级共有57名学生获奖,其中$\frac{1}{3}$的学生同时获得两种奖,已知数学竞赛获奖人数比演讲比赛获奖人数多16名,问:数学竞赛和演讲比赛各有多少名学生获奖?
19.确定一个圆的条件是( )
| A. | 已知圆心 | B. | 已知半径 | ||
| C. | 过三个已知点 | D. | 过一个三角形的三个顶点 |
20.某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的A型智能手表,去年销售总额为80000元,今年A型智能手表的售价每只比去年降了600元,若售出的数量与去年相同,销售总额将比去年减少25%.
(1)请问今年A型智能手表每只售价多少元?
(2)今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价与销售价格如右表,若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
| A型智能手表 | B型智能手表 | |
| 进价 | 1300元/只 | 1500元/只 |
| 售价 | 今年的售价 | 2300元/只 |
(2)今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价与销售价格如右表,若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
17.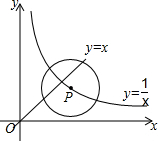 如图,点P是函数y=$\frac{1}{x}$(x>0)的图象上的一点,⊙P的半径为$\sqrt{2}$,当⊙P与直线y=x有公共点时,点P的横坐标x的取值范围是( )
如图,点P是函数y=$\frac{1}{x}$(x>0)的图象上的一点,⊙P的半径为$\sqrt{2}$,当⊙P与直线y=x有公共点时,点P的横坐标x的取值范围是( )
 如图,点P是函数y=$\frac{1}{x}$(x>0)的图象上的一点,⊙P的半径为$\sqrt{2}$,当⊙P与直线y=x有公共点时,点P的横坐标x的取值范围是( )
如图,点P是函数y=$\frac{1}{x}$(x>0)的图象上的一点,⊙P的半径为$\sqrt{2}$,当⊙P与直线y=x有公共点时,点P的横坐标x的取值范围是( )| A. | 1≤x≤$\sqrt{2}$ | B. | $\sqrt{2}-1≤x≤\sqrt{2}$ | C. | $\sqrt{2}-1≤x≤1$ | D. | $\sqrt{2}-1≤x≤\sqrt{2}+1$ |
18.一个不透明的口袋中有4个绿球和2个黄球,它们除颜色外其他都完全相同.将球摇匀后,随机摸出一球,吧剩下的球摇匀后,再随机摸出一球,两球都为绿球的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
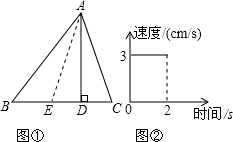 如图①,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②
如图①,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②