Question

17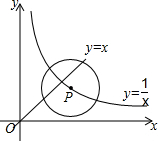．如图，点P是函数y=$\frac{1}{x}$（x＞0）的图象上的一点，⊙P的半径为$\sqrt{2}$，当⊙P与直线y=x有公共点时，点P的横坐标x的取值范围是（　　）

• A． 1≤x≤$\sqrt{2}$
• B． $\sqrt{2}-1≤x≤\sqrt{2}$
• C． $\sqrt{2}-1≤x≤1$
• D． $\sqrt{2}-1≤x≤\sqrt{2}+1$

Answer 1

分析 如图所示，P₁P₂即为⊙P与直线y=x有一个公共点的情况，点P只有在线段P₁P₂上，即符合题意，根据图象的对称性可知，△AP₁P₂是等腰直角三角形，求得AP₁=AP₂=2，设P₁（x₀，$\frac{1}{{x}_{0}}$），则P₂（x₀+2，$\frac{1}{{x}_{0}}$-2），则AP₁P₂的中点M在直线y=x上，得到M（x₀+1，$\frac{1}{{x}_{0}}$-1），解方程得到x₀=$\sqrt{2}$-1，x₀=-$\sqrt{2}$-1（不合题意，舍去），于是得到结论．

解答 解：如图所示，P₁P₂即为⊙P与直线y=x有一个公共点的情况，
点P只有在线段P₁P₂上，即符合题意，
根据图象的对称性可知，△AP₁P₂是等腰直角三角形，
∵⊙P的半径为$\sqrt{2}$，
∴P₁P₂=2$\sqrt{2}$，
∴AP₁=AP₂=2，
设P₁（x₀，$\frac{1}{{x}_{0}}$），则P₂（x₀+2，$\frac{1}{{x}_{0}}$-2），
则AP₁P₂的中点M在直线y=x上，
∴M（x₀+1，$\frac{1}{{x}_{0}}$-1），∴x₀+1=$\frac{1}{{x}_{0}}$-1，
解得：x₀=$\sqrt{2}$-1，x₀=-$\sqrt{2}$-1（不合题意，舍去），
∴P₁的横坐标是$\sqrt{2}$-1，P₂的横坐标是$\sqrt{2}$+1，
∴$\sqrt{2}$-1≤x≤$\sqrt{2}$+1，
故选D．

点评 本题考查了反比例函数与一次函数的交点问题，直线与圆的位置关系，等腰直角三角形的性质，正确的作出辅助线是解题的关键．