题目内容
7.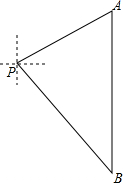 如图,一艘轮船位于灯塔P的北偏东65°方向8海里远的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东39°方向上的B处.B距离P有多远?(精确到0.1海里)
如图,一艘轮船位于灯塔P的北偏东65°方向8海里远的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东39°方向上的B处.B距离P有多远?(精确到0.1海里)
分析 过P作PC⊥AB,垂足为C,解Rt△APC,得出PC=PA•cos∠APC≈7.28.再解Rt△BPC,由PB=$\frac{PC}{sin∠B}$,代入数据计算即可.
解答 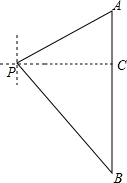 解:如图,过P作PC⊥AB,垂足为C,
解:如图,过P作PC⊥AB,垂足为C,
在Rt△APC中,∵∠APC=90°-65°=25°,
∴PC=PA•cos∠APC≈8×0.91=7.28.
在Rt△BPC中,∵∠B=39°,
∴PB=$\frac{PC}{sin∠B}$≈$\frac{7.28}{0.63}$≈11.6(海里).
答:B距离P约有11.6海里远.
点评 此题考查了解直角三角形的应用-方向角问题,三角函数的定义,正确作出辅助线构造直角三角形是解决本题的关键.

练习册系列答案
相关题目
16.一辆出租车从某地出发,在一条东西走向的接到上往返行驶,每次行驶的路程(记向东为正),记录如下(8<x<24,单位:km);
(1)说出这辆出租车每次行驶的方向;
(2)这辆出租车一共行驶了多少路程(用含x的式子表示)?
| 第一次 | 第二次 | 第三次 | 第四次 |
| x | 3(8-x) | x-6 | -$\frac{2}{3}$x |
(2)这辆出租车一共行驶了多少路程(用含x的式子表示)?

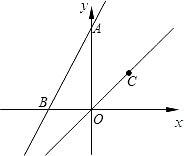 (1)直线y=2x+1绕原点旋转180°后的直线解析式为y=2x-1;
(1)直线y=2x+1绕原点旋转180°后的直线解析式为y=2x-1;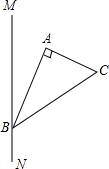 如图所示,一条南北方向的小路MN,A、B、C处各有一颗小树,且B在MN上,∠A=90°,A、C之间的距离为200米,在B处测得C在小路的北偏东55°方向上,A在小路的北偏东25°方向上,求点A到小路MN的距离.(结果精确到0.1米)
如图所示,一条南北方向的小路MN,A、B、C处各有一颗小树,且B在MN上,∠A=90°,A、C之间的距离为200米,在B处测得C在小路的北偏东55°方向上,A在小路的北偏东25°方向上,求点A到小路MN的距离.(结果精确到0.1米)