题目内容
17.(1)计算:$\sqrt{48}$$÷\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$(2)观察下列各式:
$\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$;$\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$;$\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$…,
①$\sqrt{4+\frac{1}{6}}$=5$\sqrt{\frac{1}{6}}$;$\sqrt{5+\frac{1}{7}}$=6$\sqrt{\frac{1}{7}}$.
②请用含有自然数n(n≥1)的代数式,将你猜想到的规律表达出来.
分析 (1)先根据二次根式的乘除法则运算,然后合并即可;
(2)①根据所给式子的规律填空;
②利用二次根式的性质可把$\sqrt{n+\frac{1}{n+2}}$变形为(n+1)$\sqrt{\frac{1}{n+2}}$(n≥1的整数).
解答 解:(1)原式=$\sqrt{48÷3}$-$\sqrt{\frac{1}{2}×12}$+2$\sqrt{6}$
=4-$\sqrt{6}$+2$\sqrt{6}$
=4+$\sqrt{6}$;
(2)①$\sqrt{4+\frac{1}{6}}$=5$\sqrt{\frac{1}{6}}$;$\sqrt{5+\frac{1}{7}}$=6$\sqrt{\frac{1}{7}}$;
②$\sqrt{n+\frac{1}{n+2}}$=$\sqrt{\frac{n(n+2)+1}{n+2}}$=$\sqrt{\frac{(n+1)^{2}}{n+2}}$=(n+1)$\sqrt{\frac{1}{n+2}}$(n≥1的整数).
故答案为5$\sqrt{\frac{1}{6}}$;6$\sqrt{\frac{1}{7}}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
5.如下表是七年级某班5名同学数学测试成绩,根据信息完成下列问题:
①完成表中的空格信息;
②5人中最高分是谁?最低分是谁?分数与全班平均分最接近的是谁?
①完成表中的空格信息;
②5人中最高分是谁?最低分是谁?分数与全班平均分最接近的是谁?
| 姓名 | 王芳 | 刘兵 | 张昕 | 李聪 | 江文 |
| 成绩 | 89 | 92 | 90 | 84 | 88 |
| 与全班平 均分之差 | -1 | +2 | 0 | -6 | -2 |
2.若a>b,则下列不等式的变形错误的是( )
| A. | a-8>b-8 | B. | a+5>b+5 | C. | -3a>-3b | D. | $\frac{a}{{m}^{2}+1}>\frac{b}{{m}^{2}+1}$ |
9.已知抛物线y=2x2-(m2+1)x+2m2-1,不论m取何值,抛物线恒过某定点P,则P点的坐标为( )
| A. | (2,-5) | B. | (2,5) | C. | (-2,5) | D. | 不能确定 |
6.在平面直角坐标系中,已知线段AB是两个端点分别是A(-4,-1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,2),则点B′的坐标为( )
| A. | (4,3) | B. | (3,-4) | C. | (3,4) | D. | (-2,-1) |
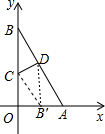 如图,△AOB中,∠AOB=90°,OA=1,OB=2.折叠纸片,使顶点B落在底边OB上的B′处,折痕为CD,若DB′⊥OA,则点B′的坐标为(2$\sqrt{5}$-4,0).
如图,△AOB中,∠AOB=90°,OA=1,OB=2.折叠纸片,使顶点B落在底边OB上的B′处,折痕为CD,若DB′⊥OA,则点B′的坐标为(2$\sqrt{5}$-4,0).