解不等式组$\left\{\begin{array}{l}{\frac{3x-3}{2}-\frac{2x+1}{3}≤x}\\{\frac{1}{2}[x-2(x-3)]＞1}\end{array}\right.$并将解集在数轴上表示出来．题目和参考答案——青夏教育精英家教网—

题目内容

12．解不等式组$\left\{\begin{array}{l}{\frac{3x-3}{2}-\frac{2x+1}{3}≤x}\\{\frac{1}{2}[x-2（x-3）]＞1}\end{array}\right.$并将解集在数轴上表示出来．

分析分别求出各不等式的解集，再求出其公共解集并在数轴上表示出来即可．

解答解：$\left\{\begin{array}{l}\frac{3x-3}{2}-\frac{2x+1}{3}≤x①\\ \frac{1}{2}[x-2（x-3）]＞1②\end{array}\right.$，由①得，x≥-11，由②得，x＜4，
故不等式组的解集为-11≤x＜4．
在数轴上表示为：
．

点评本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．

练习册系列答案

相关题目

2．

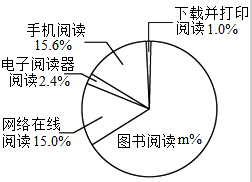根据某研究院公布的2010-2014年我国成年国民阅读调查报告的部分相关数据，绘制的统计图表如下：

年份	年人均阅读图书数量（本）
2010	3.8
2011	4.1
2012	4.3
2013	4.6
2014	4.8

根据以上信息解答下列问题：
（1）直接写出扇形统计图中m的值；
（2）从2010到2014年，成年居民年人均阅读图书的数量每年增长的幅度近似相等，用这五年间平均增幅量来估算2015年成年居民年人均阅读图书的数量约为5本；
（3）2014年某小区倾向图书阅读的成年居民有1000人，若该小区2015年与2014年成年居民的人数基本持平，估算2015年该小区成年国民阅读图书的总数量约为7576本．

3．观察算式$\frac{-5+\sqrt{{5}^{2}-4×2×3}}{2×2}$+$\frac{-5-\sqrt{{5}^{2}-4×2×3}}{2×2}$，计算它得到的结果是-$\frac{5}{2}$．

20．若A（x₁，y₁）、B（x₂，y₂）是一次函数y=ax-2x+1图象上的不同的两个点，记m=（x₁-x₂）（y₁-y₂），则当m＜0时，a的取值范围是（　　）

7．将（a+b）（c+d）展开后是4个单项式的和；将（a+b）（c+d+e）展开后是6个单项式的和；将（a+b+c）（d+e+f）展开后是9个单项式的和；…，以此类推，将（a₁+a₂+a₃+…+a_m）（b₁+b₂+b₃+…+b_n）展开
后是mn个单项式的和．

17．（1）计算：$\sqrt{48}$$÷\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$
（2）观察下列各式：
$\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$；$\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$；$\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$…，
①$\sqrt{4+\frac{1}{6}}$=5$\sqrt{\frac{1}{6}}$；$\sqrt{5+\frac{1}{7}}$=6$\sqrt{\frac{1}{7}}$．
②请用含有自然数n（n≥1）的代数式，将你猜想到的规律表达出来．

4．解方程组：$\left\{\begin{array}{l}{2x+y=1①}\\{2x-3y=-19②}\end{array}\right.$．

1．若a：b=3：5，且b是a、c的比例中项，那么b：c的值是（　　）

2．

如图，三角形DEF是由三角形ABC通过平移得到，且点B，E，C，F在同一条直线上，若BF=14，EC=6，则BE的长度是4．

试题分类