题目内容
9.已知抛物线y=2x2-(m2+1)x+2m2-1,不论m取何值,抛物线恒过某定点P,则P点的坐标为( )| A. | (2,-5) | B. | (2,5) | C. | (-2,5) | D. | 不能确定 |
分析 令m=0,则y=2x2-x-1,令m=1,则y=2x2-2x+1,联立方程,解方程即可求得P的坐标.
解答 解:∵不论m取何值,抛物线恒过某定点P,
∴令m=0,则y=2x2-x-1,令m=1,则y=2x2-2x+1,
解$\left\{\begin{array}{l}{y=2{x}^{2}-x-1}\\{y=2{x}^{2}-2x+1}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$
∴P的坐标为(2,5),
故选B.
点评 本题考查了二次函数图象上点的坐标特征,根据题意列出方程组是解题的关键.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
19.下列计算结果正确的是( )
| A. | x•x2=x2 | B. | (ab)3=a3b3 | C. | (x5)3=x8 | D. | a6÷a2=a3 |
20.若A(x1,y1)、B(x2,y2)是一次函数y=ax-2x+1图象上的不同的两个点,记m=(x1-x2)(y1-y2),则当m<0时,a的取值范围是( )
| A. | a<0 | B. | a>0 | C. | a<2 | D. | a>2 |
1.若a:b=3:5,且b是a、c的比例中项,那么b:c的值是( )
| A. | 3:2 | B. | 5:3 | C. | 3:5 | D. | 2:3 |
19.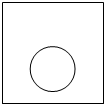 如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
 如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )| A. | πr2 | B. | a2-πr2 | C. | 4r2-πr2 | D. | $\frac{a^2}{4}$ |