题目内容
6.在平面直角坐标系中,已知线段AB是两个端点分别是A(-4,-1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,2),则点B′的坐标为( )| A. | (4,3) | B. | (3,-4) | C. | (3,4) | D. | (-2,-1) |
分析 各对应点之间的关系是横坐标加2,纵坐标加3,那么让点B的横坐标加2,纵坐标加3即为点B′的坐标.
解答 解:∵A(-4,-1)的对应点A′的坐标为(-2,2 ),
∴坐标的变化规律为:各对应点之间的关系是横坐标加2,纵坐标加3,
∴点B′的横坐标为1+2=3;纵坐标为1+3=4,
即所求点B′的坐标为(3,4).
故选C.
点评 此题主要考查了坐标与图形的变化-平移,解决本题的关键是根据已知对应点找到各对应点之间的变化规律.

练习册系列答案
相关题目
16.在函数y=-$\frac{1}{x}$的图象上有三点(-3,y1),(-1,y2),(2,y3),则( )
| A. | y3<y1<y2 | B. | y2<y3<y1 | C. | y3<y1<y2 | D. | y1<y2<y3 |
1.若a:b=3:5,且b是a、c的比例中项,那么b:c的值是( )
| A. | 3:2 | B. | 5:3 | C. | 3:5 | D. | 2:3 |
16.已知方程$\frac{x}{2}-\frac{y}{3}=5$,用含x的代数式表示y,下列给出的结论中正确的是( )
| A. | $x=\frac{2y}{3}+10$ | B. | $y=\frac{3x}{2}-15$ | C. | $y=\frac{3x-15}{2}$ | D. | $y=-\frac{3x}{2}+15$ |
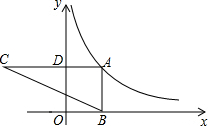 如图,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使CD=2AD,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为6,则k的值为4.
如图,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使CD=2AD,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为6,则k的值为4.