题目内容
11．设k=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$，且a＞b＞0，则有（ ）| A． | k＞2 | B． | 1＜k＜2 | C． | $\frac{1}{2}$＜k＜1 | D． | 0＜k＜$\frac{1}{2}$ |
分析 把分子、分母分别分解因式，进行约分，即可解答．
解答 解：k=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$=$\frac{（a+b）（a-b）}{a（a-b）}=\frac{a+b}{a}=1+\frac{b}{a}$，
∵a＞b＞0，
∴0＜$\frac{b}{a}＜1$，
∴1＜1+$\frac{b}{a}$＜2．
故选：B．
点评 本题考查了约分，解决本题的关键是分子、分母分别分解因式进行约分．
练习册系列答案
名校课堂系列答案
相关题目
已知：如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足是D，BC=$\sqrt{6}$，BD=1．求AD=5．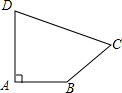
如图所示的四边形ABCD中，其中AB=3，BC=12，CD=13，DA=4，∠A=90°，你能求出四边形ABCD的面积吗？