题目内容
16．已知一个四位数M的千位数字是a，百位数字是b、十位数字是4、个位数字是c，另有一个三位数N的百位数字是（b+1）、十位数字是a、个位数字是（c-2）．请说明在所有符合要求的数中，M与N的差与b，c的取值无关，并直接写出M-N的最小值．分析 根据数的表示方法：千位数字×1000+百位数字×100+十位数字×10+个位数字，表示出M与N，作差即可．
解答 解：∵M-N=（1000a+100b+40+c）-[100（b+1）+10a+（c-2）]
=1000a+100b+40+c-100b-100-10a-c+2
=990a-58
∴M与N的差与b，c的取值无关．
当a=1时，M-N的最小值为932．
点评 本题考查了整式的加减，解决本题的关键是进行整式的加法计算．
练习册系列答案
相关题目
7．先化简，再求值：$\frac{2}{x-1}$-$\frac{x-2}{{x}^{2}-1}$÷$\frac{{x}^{2}-2x}{{x}^{2}+2x+1}$，其中，x满足x2-2x-3=0．
11．设k=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$，且a＞b＞0，则有（ ）
| A． | k＞2 | B． | 1＜k＜2 | C． | $\frac{1}{2}$＜k＜1 | D． | 0＜k＜$\frac{1}{2}$ |
2．
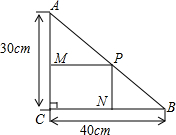如图，在Rt△ABC的内部作一个矩形CMPN，其中CM、CN分别在两直角边上，设CM=xcm，那么CN的长为（ ）
如图，在Rt△ABC的内部作一个矩形CMPN，其中CM、CN分别在两直角边上，设CM=xcm，那么CN的长为（ ）| A． | 40-$\frac{4}{3}$x | B． | 40-$\frac{3}{2}$x | C． | 30-$\frac{4}{3}$x | D． | 30-$\frac{3}{4}$x |