题目内容
2.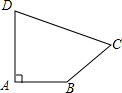 如图所示的四边形ABCD中,其中AB=3,BC=12,CD=13,DA=4,∠A=90°,你能求出四边形ABCD的面积吗?
如图所示的四边形ABCD中,其中AB=3,BC=12,CD=13,DA=4,∠A=90°,你能求出四边形ABCD的面积吗?
分析 先根据勾股定理求出BD的长度,再根据勾股定理的逆定理判断出△BCD的形状,再利用三角形的面积公式求解即可.
解答 解:能求出四边形ABCD的面积为36;理由如下:
连接BD,如图所示: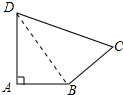
∵∠A=90°,AB=3,AD=4,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
在△BCD中,∵BD2+BC2=25+144=169=CD2,
∴△BCD是直角三角形,∠DBC=90°,
∴S四边形ABCD=$\frac{1}{2}$AB•AD+$\frac{1}{2}$BD•BC,
=$\frac{1}{2}$×3×4+$\frac{1}{2}$×5×12,
=36.
答:四边形ABCD的面积是36.
点评 本题考查了勾股定理、勾股定理的逆定理及三角形的面积;能根据勾股定理的逆定理判断出△BCD的形状是解答此题的关键.

练习册系列答案
相关题目
7.先化简,再求值:$\frac{2}{x-1}$-$\frac{x-2}{{x}^{2}-1}$÷$\frac{{x}^{2}-2x}{{x}^{2}+2x+1}$,其中,x满足x2-2x-3=0.
11.设k=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$,且a>b>0,则有( )
| A. | k>2 | B. | 1<k<2 | C. | $\frac{1}{2}$<k<1 | D. | 0<k<$\frac{1}{2}$ |
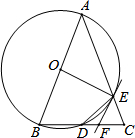 如图,AB是⊙O直径,AB=AC,BC、AC分别与⊙O相交于点D、E,EF是⊙O的切线,且与BC相交于点F.已知∠EDC=50°,则∠EFC=75°.
如图,AB是⊙O直径,AB=AC,BC、AC分别与⊙O相交于点D、E,EF是⊙O的切线,且与BC相交于点F.已知∠EDC=50°,则∠EFC=75°.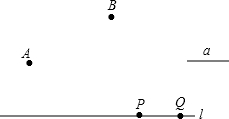 如图,A、B是直线l同侧的两定点,定长线段PQ=a在l上平行移动,请问:PQ移动到什么位置时,AP+PQ+QB的长最短?请保留作图痕迹,并写出简要的作法.
如图,A、B是直线l同侧的两定点,定长线段PQ=a在l上平行移动,请问:PQ移动到什么位置时,AP+PQ+QB的长最短?请保留作图痕迹,并写出简要的作法.