题目内容
17.在Rt△ABC中,∠C=90°,BC=8,sinA=$\frac{4}{5}$,则cosA=$\frac{3}{5}$,tanB=$\frac{3}{4}$.分析 根据已知结合锐角三角函数关系得出AB,AC的长,进而求出cosA,tanB的值.
解答 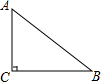 解:如图所示:∵∠C=90°,BC=8,sinA=$\frac{4}{5}$,
解:如图所示:∵∠C=90°,BC=8,sinA=$\frac{4}{5}$,
∴$\frac{BC}{AB}$=$\frac{8}{AB}$=$\frac{4}{5}$,
∴AB=10,
∴AC=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴cosA=$\frac{AC}{AB}$=$\frac{6}{10}$=$\frac{3}{5}$,
tanB=$\frac{AC}{BC}$=$\frac{6}{8}$=$\frac{3}{4}$.
故答案为:$\frac{3}{5}$,$\frac{3}{4}$.
点评 此题主要考查了锐角三角函数关系以及勾股定理,正确记忆直角三角形中边角关系是解题关键.

练习册系列答案
相关题目
11.设k=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$,且a>b>0,则有( )
| A. | k>2 | B. | 1<k<2 | C. | $\frac{1}{2}$<k<1 | D. | 0<k<$\frac{1}{2}$ |
12.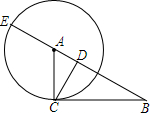 在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )
在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )
 在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )
在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.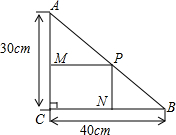 如图,在Rt△ABC的内部作一个矩形CMPN,其中CM、CN分别在两直角边上,设CM=xcm,那么CN的长为( )
如图,在Rt△ABC的内部作一个矩形CMPN,其中CM、CN分别在两直角边上,设CM=xcm,那么CN的长为( )
 如图,在Rt△ABC的内部作一个矩形CMPN,其中CM、CN分别在两直角边上,设CM=xcm,那么CN的长为( )
如图,在Rt△ABC的内部作一个矩形CMPN,其中CM、CN分别在两直角边上,设CM=xcm,那么CN的长为( )| A. | 40-$\frac{4}{3}$x | B. | 40-$\frac{3}{2}$x | C. | 30-$\frac{4}{3}$x | D. | 30-$\frac{3}{4}$x |
9.下列各数中,属于无理数的是( )
| A. | $\root{3}{8}$ | B. | $\sqrt{8}$ | C. | $\frac{22}{7}$ | D. | 3.1415926 |
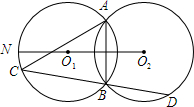 已知:两等圆⊙O1与⊙O2相交于点A、B,若点O1在⊙O2外,延长O2O1交⊙O1于点N,在劣弧$\widehat{NB}$上任取一点C(点C与点B不重合),CB的延长线交⊙O2于点D,如图所示,连结AC,试比较AC与AB的大小.
已知:两等圆⊙O1与⊙O2相交于点A、B,若点O1在⊙O2外,延长O2O1交⊙O1于点N,在劣弧$\widehat{NB}$上任取一点C(点C与点B不重合),CB的延长线交⊙O2于点D,如图所示,连结AC,试比较AC与AB的大小.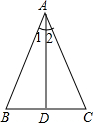 如图,在△ABC中,AB=AC,AD⊥BC于D.求证:BD=CD,∠1=∠2.
如图,在△ABC中,AB=AC,AD⊥BC于D.求证:BD=CD,∠1=∠2.