题目内容
6.甲、乙两地相距180千米,已知轮船在静水中的航速是每小时a千米,水流速度是每小时10千米,若轮船从甲地顺流航行3小时到达乙地后立刻逆流返航,则逆流行驶1小时后离甲地的距离是40千米.分析 先根据顺流航行的速度×顺流航行的时间=180千米,列出方程,求出a的值;再求出轮船逆流行驶1小时的路程,即为所求.
解答 解:由轮船在静水中的航速是a千米/时,水流速度是10千米/时,
则轮船顺流航行的速度为(a+10)千米/时.
由题意,知3(a+10)=180,
解得:a=50.
轮船逆流航行的速度为:a-10=50-10=40(千米/时),
轮船逆流行驶1小时后离乙地的距离是:1×40=40(千米).
故答案为:40.
点评 本题考查一元一次方程在行程问题中的应用.关键是知道如何求顺流和逆流的速度,如何根据速度、路程、时间列出方程解决问题.注意:顺流速度=静水速度+水流速度;逆流速度=静水速度-水流速度.

练习册系列答案
相关题目
11.设k=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$,且a>b>0,则有( )
| A. | k>2 | B. | 1<k<2 | C. | $\frac{1}{2}$<k<1 | D. | 0<k<$\frac{1}{2}$ |
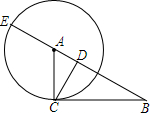 在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )
在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )