题目内容
14.先化简,再求值:($\frac{a-2}{{a}^{2}+2a}-\frac{a-1}{{a}^{2}+4a}$)÷$\frac{a-4}{a+2}$,其中a=3.分析 先根据分式的混合运算顺序和法则化简原式,再将a的值代入计算即可.
解答 解:原式=[$\frac{a-2}{a(a+2)}$-$\frac{a-1}{a(a+4)}$]•$\frac{a+2}{a-4}$
=$\frac{a-2}{a(a+2)}$•$\frac{a+2}{a-4}$-$\frac{a-1}{a(a+4)}$•$\frac{a+2}{a-4}$
=$\frac{a-2}{a(a-4)}$-$\frac{{a}^{2}+a-2}{a(a+4)(a-4)}$
=$\frac{{a}^{2}+2a-8}{a(a+4)(a-4)}$-$\frac{{a}^{2}+a-2}{a(a+4)(a-4)}$
=$\frac{a-6}{a(a+4)(a-4)}$,
当a=3时,
原式=$\frac{-3}{3×7×(-1)}$=$\frac{1}{7}$.
点评 本题主要考查分数的化简求值,熟练掌握分式的混合运算顺序和法则是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.用相同边长的正三角形和正方形进行镶嵌,若每一个顶点周围有m个正三角形和n个正方形.则m,n满足的关系是( )
| A. | 2m+3n=12 | B. | m+n=7 | C. | 2m+n=6 | D. | m+2n=6 |
 如图,将一根长24厘米的筷子,置于底面直径为6厘米,高为8厘米的圆柱形水杯中,则筷子露在杯子外面的长度至少为多少厘米?
如图,将一根长24厘米的筷子,置于底面直径为6厘米,高为8厘米的圆柱形水杯中,则筷子露在杯子外面的长度至少为多少厘米?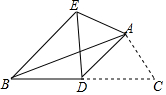 如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿AD所在直线对折,点C落在点E的位置,求∠EBC的度数.
如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿AD所在直线对折,点C落在点E的位置,求∠EBC的度数.