题目内容
14.关于x的一元二次方程x2+2x+m+3=0的两个实数根分别为x1,x2.(1)求m的取值范围;
(2)若2(x1+x2)+x12x22-32=0,求m的值.
分析 (1)根据一元二次方程x2+2x+m+3=0的两个实数根得到△=4-4(m+3)≥0,求出m的取值范围即可;
(2)首先根据根与系数的关系求出x1+x2=-2,x1•x2=m+3,然后得到关于m的一元二次方程,求出m的值即可.
解答 解:(1)∵关于x的一元二次方程x2+2x+m+3=0的两个实数根,
∴△≥0,即4-4(m+3)≥0,
∴m≤-2;
(2)∵关于x的一元二次方程x2+2x+m+3=0的两个实数根分别为x1,x2,
∴x1+x2=-2,x1•x2=m+3,
∵2(x1+x2)+x12x22-32=0,
∴2×(-2)+(m+3)2-32=0,即(m+3)2=36,
∴m1=-9,m2=3,
∵由(1)m≤-2,
∴m=-9.
点评 本题主要考查了根的判别式以及根与系数的关系的知识,解答本题的关键是熟练掌握根的判别式的意义求出m的取值范围,此题难度不大.

练习册系列答案
相关题目
5.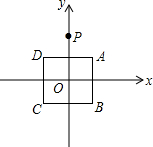 正方形ABCD在坐标系中位置如图所示,作点P(0,2)关于点A的对称点P1,点P1关于点B的对称点P2,点P2关于点C的对称点P3,点P3关于点D的对称点P4,…,按此操作下去,则点P2014的坐标为( )
正方形ABCD在坐标系中位置如图所示,作点P(0,2)关于点A的对称点P1,点P1关于点B的对称点P2,点P2关于点C的对称点P3,点P3关于点D的对称点P4,…,按此操作下去,则点P2014的坐标为( )
 正方形ABCD在坐标系中位置如图所示,作点P(0,2)关于点A的对称点P1,点P1关于点B的对称点P2,点P2关于点C的对称点P3,点P3关于点D的对称点P4,…,按此操作下去,则点P2014的坐标为( )
正方形ABCD在坐标系中位置如图所示,作点P(0,2)关于点A的对称点P1,点P1关于点B的对称点P2,点P2关于点C的对称点P3,点P3关于点D的对称点P4,…,按此操作下去,则点P2014的坐标为( )| A. | (0,2) | B. | (2,0) | C. | (0,-2) | D. | (-2,0) |
2. 如图是正方体的平面展开图,每个面上标有一个汉字,与“我”字相对的面上的字是( )
如图是正方体的平面展开图,每个面上标有一个汉字,与“我”字相对的面上的字是( )
 如图是正方体的平面展开图,每个面上标有一个汉字,与“我”字相对的面上的字是( )
如图是正方体的平面展开图,每个面上标有一个汉字,与“我”字相对的面上的字是( )| A. | 魅 | B. | 力 | C. | 绵 | D. | 阳 |
9.下列命题错误的是( )
| A. | 角平分线上的点到角的两边的距离相等 | |
| B. | 圆的切线垂直于过切点的直径 | |
| C. | 多边形外角和等于360° | |
| D. | 相似图形一定是位似图形 |
18.下列运算正确的是( )
| A. | a3•a2=a6 | B. | a3÷a2=a${\;}^{\frac{3}{2}}$ | C. | a3-a2=a | D. | (a+1)2=a2+2a+1 |
 如图,已知AB∥CD,∠BAE=40°,∠ECD=70°,EF平分∠AEC,则∠AEF的度数是55°.
如图,已知AB∥CD,∠BAE=40°,∠ECD=70°,EF平分∠AEC,则∠AEF的度数是55°.