题目内容
12.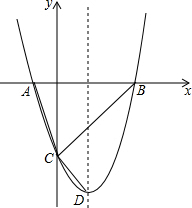 如图,抛物线y=x2-(2m+4)x+m2+4m交x轴于点A,B(点A在点B左侧),交y轴于点C,其顶点为D.
如图,抛物线y=x2-(2m+4)x+m2+4m交x轴于点A,B(点A在点B左侧),交y轴于点C,其顶点为D.(1)求AB的长;
(2)连接CD,BC,当∠BCD=90°时,求抛物线解析式;
(3)连接AC,在(2)的前提下,在抛物线上是否存在点T,使得∠BCT+∠ACO=∠BAC?若存在,求出点T坐标;若不存在,写出理由.
分析 (1)由点A,B在x轴上,求出点A,B的坐标即可;
(2)点C,D的坐标表示出来,用△MCD∽△OBC得到$\frac{OB}{CM}$=$\frac{OC}{MD}$,代入即可;
(3)先求出AN,再确定出直线CW的解析式为y=-$\frac{1}{7}$x-3,和抛物线y=x2-2x-3联立方程组即可.
解答 解:(1)令y=0,
∴x2-(2m+4)x+m2+4m=0,
∴x1=m,x2=m+4,
∴A(m,0),B(m+4,0),
∴AB=4,
(2)如图1,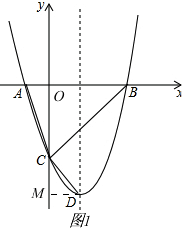
过点D作DM⊥y轴,C(0,m2+4m),D(m+2,-4),
∵∠BCD=90°,∠BOC=90°,
∴∠MCD=∠OBC,∠MDC=∠OCB,
∴△MCD∽△OBC,
∴$\frac{OB}{CM}$=$\frac{OC}{MD}$,
∴$\frac{m+4}{{m}^{2}+4m+4}=\frac{-{m}^{2}-4m}{m+2}$,
∴m1=m2=-1,
∴y=x2-2x-3;
(3)存在;
如图2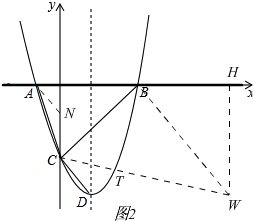
作∠CAN=∠ACO,
∴AN=CN,
∵∠BCT=∠ACO=∠BAC,
∴∠BCT=∠OAN,
∴A(-1,0),B(3,0),C(0,-3),
在Rt△AON中,OA=1,设ON=a,
∴AN=CN=3-a,
∴(3-a)2=12+a2,
∴ON=a=$\frac{4}{3}$
假设抛物线上存在点T,过点B作BW⊥BC,交CT的延长线于W,过W作WH⊥x轴,
∴$\frac{BW}{BC}$=$\frac{ON}{OA}$=$\frac{4}{3}$,
∴BW=4$\sqrt{2}$,BH=HW=4,
∴W(7,-4),直线CW的解析式为y=-$\frac{1}{7}$x-3,
$\left\{\begin{array}{l}{y={x}^{2}-2x-3}\\{y=-\frac{1}{7}x-3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}_{1}=\frac{13}{7}}\\{{y}_{1}=\frac{160}{49}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=0}\\{{y}_{2}=-3}\end{array}\right.$(舍),
∴T1($\frac{13}{7}$,$\frac{160}{49}$),
同理可得:T2(-5,32).
即:抛物线上是存在点T,使得∠BCT+∠ACO=∠BAC,点T1($\frac{13}{7}$,$\frac{160}{49}$),T2(-5,32).
点评 此题是二次函数综合题,主要考查相似三角形的性质和判定,勾股定理,确定图象交点坐标,作出辅助线是解本题的关键,也是难点.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案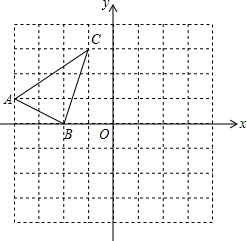 (1)请你把△ABC平移到△DEF,使点A(-4,1)的对应点D的坐标为(1,-2),B、C的对应点分别为E、F.
(1)请你把△ABC平移到△DEF,使点A(-4,1)的对应点D的坐标为(1,-2),B、C的对应点分别为E、F. 如图,在△ABC中,AB=AC,AD⊥BC,交BC于D,BD=5cm,求底边BC的长.
如图,在△ABC中,AB=AC,AD⊥BC,交BC于D,BD=5cm,求底边BC的长. 如图,在?ABCD中,O为BD的中点,过O作两条互相垂直的直线,分别交四边形ABCD于E,F,G,H,求证:四边形EFGH是菱形.
如图,在?ABCD中,O为BD的中点,过O作两条互相垂直的直线,分别交四边形ABCD于E,F,G,H,求证:四边形EFGH是菱形.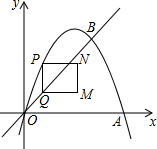 如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于O、A两点,与直线y=x交于点B,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,过点P作y轴的平行线交射线OB于点Q,以PQ为边向右作矩形PQMN,且PN=1,设点P的横坐标为m(m>0,且m≠2).
如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于O、A两点,与直线y=x交于点B,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,过点P作y轴的平行线交射线OB于点Q,以PQ为边向右作矩形PQMN,且PN=1,设点P的横坐标为m(m>0,且m≠2).