题目内容
4.在实数范围内分解因式:2x4-18=2(x2+3)(x+$\sqrt{3}$)(x-$\sqrt{3}$).分析 先将多项式变形为2[(x2)2-32],套用公式a2-b2=(a+b)(a-b)进行分解因式,然后再进一步套用公式进行因式分解.
解答 解:原式=2(x4-9)
=2(x2+3)(x2-3)
=2(x2+3)(x+$\sqrt{3}$)(x-$\sqrt{3}$),
故答案为:$2(x+\sqrt{3})(x-\sqrt{3})({x^2}+3)$.
点评 本题考查了用公式法进行因式分解的能力,若在实数范围内分解因式,因式分解要彻底,直到不能分解为止.

练习册系列答案
相关题目
15.下列实数是无理数的是( )
| A. | -$\sqrt{5}$ | B. | 0 | C. | $\frac{1}{3}$ | D. | 6 |
9.若$\root{3}{0.3670}$=0.7160,$\root{3}{3.670}$=1.542,则$\root{3}{367}$=7.16,$\root{3}{-3670}$=-15.42.
14.将点A(-4,-2)向右平移5的单位长度得到点B,则点B的所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
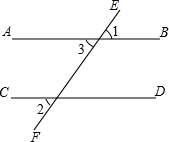 (1)如图,已知直线EF与AB、CD都相交,AB∥CD.
(1)如图,已知直线EF与AB、CD都相交,AB∥CD.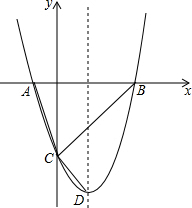 如图,抛物线y=x2-(2m+4)x+m2+4m交x轴于点A,B(点A在点B左侧),交y轴于点C,其顶点为D.
如图,抛物线y=x2-(2m+4)x+m2+4m交x轴于点A,B(点A在点B左侧),交y轴于点C,其顶点为D.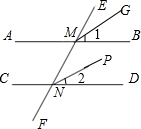 如图,直线AB和直线CD被直线EF所截,∠BMN=∠DNF,∠1=∠2,那么MG与NP平行吗?请说明理由.
如图,直线AB和直线CD被直线EF所截,∠BMN=∠DNF,∠1=∠2,那么MG与NP平行吗?请说明理由.