题目内容
11.已知a-2b=3.求9-2a+4b的值.分析 首先依据等式的性质求得-2a+4b的值,然后代入计算即可.
解答 解:∵a-2b=3,
∴-2a+4b=-6.
∴9-2a+4b=9+(-6)=3.
点评 本题主要考查的是求代数式的值,依据等式的性质求得-2a+4b的值是解题的关键.

练习册系列答案
相关题目
1. 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究.探究过程如下,请补充完整.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究.探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:
其中,m=0,n=0.
(2)根据表格数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分.
(3)观察函数图象,写出两条函数的性质:①函数图象是轴对称图形,关于y轴对称;②当x>1时,y随x的增大而增大.
(4)进一步探究函数图象发现:
①函数图象与x轴有3个交点,所以对应的方程x2-2|x|=0有3个实数根;
②方程x2-2|x|=2有2个实数根.
 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究.探究过程如下,请补充完整.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究.探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:
| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | 3 | $\frac{5}{4}$ | m | -1 | 0 | -1 | n | $\frac{5}{4}$ | 3 | … |
(2)根据表格数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分.
(3)观察函数图象,写出两条函数的性质:①函数图象是轴对称图形,关于y轴对称;②当x>1时,y随x的增大而增大.
(4)进一步探究函数图象发现:
①函数图象与x轴有3个交点,所以对应的方程x2-2|x|=0有3个实数根;
②方程x2-2|x|=2有2个实数根.
19.过以下四边形的四个顶点不能作一个圆的是( )
| A. |  等腰梯形 | B. |  矩形 | ||
| C. |  直角梯形 | D. |  对角是90°的四边形 |
6.下列二次根式中,是最简二次根式的为( )
| A. | $\sqrt{7}$ | B. | $\sqrt{18}$ | C. | $\sqrt{x^2}$ | D. | $\sqrt{\frac{1}{3}}$ |
20.抛物线y=2x2-2$\sqrt{2}$x+1与x轴的交点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
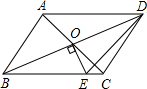 如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则AB+AD的值是( )
如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则AB+AD的值是( ) 如图,已知AB∥CD,CF∥BE,OB=OC,求证:AE=DF.
如图,已知AB∥CD,CF∥BE,OB=OC,求证:AE=DF.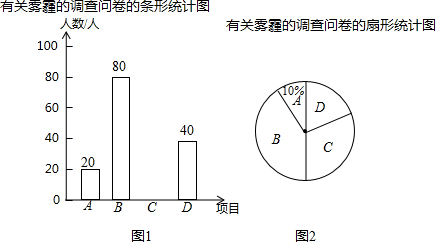 某市对市民看展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:
某市对市民看展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项: