题目内容
 已知CA、BE分别垂直AB于A点和B点,∠CDE=90°,
已知CA、BE分别垂直AB于A点和B点,∠CDE=90°,(1)求证:△CAD∽△DBE;
(2)若CA=2,AD=3,BE=6,求DB的长.
考点:相似三角形的判定与性质
专题:
分析:(1)如图,首先证明∠EDB=∠C,证明∠B=∠A,即可解决问题.
(2)如图,由△CAD∽△DBE,列出比例式
=
,求出DB即可解决问题.
(2)如图,由△CAD∽△DBE,列出比例式
| CA |
| DB |
| AD |
| BE |
解答: (1)证明:如图,∵∠CDE=90°,
(1)证明:如图,∵∠CDE=90°,
∴∠CDA+∠EDB=90°;
∵CA⊥AB,
∴∠A=90°,
∴∠CDA+∠C=90°,
∴∠EDB=∠C;
∵EB⊥AB,
∴∠B=90°=∠A,
∴△CAD∽△DBE.
(2)解:∵△CAD∽△DBE,
∴
=
,
∵CA=2,AD=3,BE=6
∴
=
,
∴DB=4.
 (1)证明:如图,∵∠CDE=90°,
(1)证明:如图,∵∠CDE=90°,∴∠CDA+∠EDB=90°;
∵CA⊥AB,
∴∠A=90°,
∴∠CDA+∠C=90°,
∴∠EDB=∠C;
∵EB⊥AB,
∴∠B=90°=∠A,
∴△CAD∽△DBE.
(2)解:∵△CAD∽△DBE,
∴
| CA |
| DB |
| AD |
| BE |
∵CA=2,AD=3,BE=6
∴
| 2 |
| DB |
| 3 |
| 6 |
∴DB=4.
点评:该题主要考查了相似三角形的判定及其性质等知识点及其应用问题;解题的关键是牢固掌握相似三角形的判定及其性质,这是灵活解题的基础和关键.

练习册系列答案
相关题目
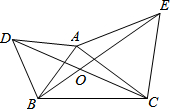 如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是
如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是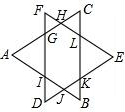 如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6.
如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6.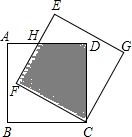 如图,边长为3的正方形ABCD终点C按顺时针旋转30°,得到正方形EFCG,交AD于点H,则阴影部分的面积为
如图,边长为3的正方形ABCD终点C按顺时针旋转30°,得到正方形EFCG,交AD于点H,则阴影部分的面积为 (1)将半圆绕它的直径旋转一周形成的几何体是
(1)将半圆绕它的直径旋转一周形成的几何体是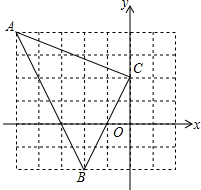 已知,如图点A(-5,4),B(-2,-2),C(0,2),求△ABC的周长.
已知,如图点A(-5,4),B(-2,-2),C(0,2),求△ABC的周长. 已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AB=10,BC=6.求:sin∠ACD的值及AD的长.
已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AB=10,BC=6.求:sin∠ACD的值及AD的长.