题目内容
 如图,已知AB、AC为⊙O的两条弦,D、E分别是
如图,已知AB、AC为⊙O的两条弦,D、E分别是 |
| AB |
 |
| AC |
(1)AF=AG;
(2)AF2=DF•EG.
考点:相似三角形的判定与性质,圆心角、弧、弦的关系
专题:证明题
分析:(1)连接OD交AB于M,连接OE交AC于N,易证∠ODE=∠OED和∠DFB=∠EGC,即可求得∠AFG=∠AGF,可得AF=AG;
(2)连接AD、AE,先证明△ADF∽△AEG,得出比例式AF:DF=EG:AG,得AF×AG=DF×EG,再由AF=AG,即可证出结论.
(2)连接AD、AE,先证明△ADF∽△AEG,得出比例式AF:DF=EG:AG,得AF×AG=DF×EG,再由AF=AG,即可证出结论.
解答:证明:(1)连接OD交AB于M,连接OE交AC于N,如图所示:
∵OD=OE,∴∠ODE=∠OED,
∵D、E分别是
、
的中点,
∴OD⊥AB,OE⊥AC,
∴∠ODE+∠DFB=90°,∠OED+∠EGC=90°,
∴∠DFB=∠EGC,
∵∠AFG=∠DFB,∠AGF=∠EGC,
∴∠AFG=∠AGF,
∴AF=AG;
(2)连接AD、AE,
由(1)得:∠AFG=∠AGF,
∴∠AFD=∠EGA,
∵D是
的中点,
∴
=
,
∴∠DAF=∠AEG,
∴△ADF∽△AEG,
∴AF:DF=EG:AG
∴AF×AG=DF×EG
又∵AF=AG
∴AF2=DF×EG

∵OD=OE,∴∠ODE=∠OED,
∵D、E分别是
 |
| AB |
 |
| AC |
∴OD⊥AB,OE⊥AC,
∴∠ODE+∠DFB=90°,∠OED+∠EGC=90°,
∴∠DFB=∠EGC,
∵∠AFG=∠DFB,∠AGF=∠EGC,
∴∠AFG=∠AGF,
∴AF=AG;
(2)连接AD、AE,
由(1)得:∠AFG=∠AGF,
∴∠AFD=∠EGA,
∵D是
 |
| AB |
∴
 |
| BD |
 |
| AD |
∴∠DAF=∠AEG,
∴△ADF∽△AEG,
∴AF:DF=EG:AG
∴AF×AG=DF×EG
又∵AF=AG
∴AF2=DF×EG
点评:本题考查了相似三角形的判定与性质、垂径定理、圆周角定理;培养学生综合运用定理进行推理论证的能力,证明角相等是解题的关键.

练习册系列答案
相关题目
某市2013年全年商品房销售面积约2596000平方米,用科学记数法表示为( )平方米.
| A、0.2596×107 |
| B、2.596×106 |
| C、2.596×107 |
| D、25.96×105 |
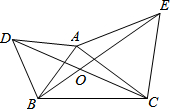 如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是
如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是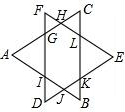 如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6.
如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6. (1)将半圆绕它的直径旋转一周形成的几何体是
(1)将半圆绕它的直径旋转一周形成的几何体是 如图所示,O是直线AB上一点,∠AOC:∠BOC=1:2,∠COD:∠AOC=1:2.
如图所示,O是直线AB上一点,∠AOC:∠BOC=1:2,∠COD:∠AOC=1:2.