题目内容
4．在△ABC中，∠C=90°，若∠A=30°，则sinA+cosB的值等于（ ）| A． | 1 | B． | $\frac{1-\sqrt{3}}{2}$ | C． | $\frac{1+\sqrt{3}}{2}$ | D． | $\frac{1}{4}$ |
分析 根据特殊角三角函数值，可得答案．
解答 解：在△ABC中，∠C=90°，若∠A=30°，得
∠B=90°-30°=60°．
sinA+cosB=sin30°+cos60°=$\frac{1}{2}$+$\frac{1}{2}$=1，
故选：A．
点评 本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键．
练习册系列答案
相关题目
14．
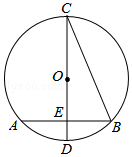如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC，若AB=2$\sqrt{2}$cm，∠BCD=22°30′，则⊙O的半径为（ ）
如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC，若AB=2$\sqrt{2}$cm，∠BCD=22°30′，则⊙O的半径为（ ）| A． | 4cm | B． | 3cm | C． | 2cm | D． | 1cm |
12．等腰三角形的腰长是4，底边长为3，那么周长是（ ）
| A． | 11 | B． | 10 | C． | 8 | D． | 7 |
19．
如图，△ABC中，AB=AC，点D在AC边上（不包括点A和点C），BD=BA，设∠A=x度，则x的取值范围是（ ）
如图，△ABC中，AB=AC，点D在AC边上（不包括点A和点C），BD=BA，设∠A=x度，则x的取值范围是（ ）| A． | 30＜x＜45 | B． | 45＜x＜60 | C． | 60＜x＜90 | D． | 90＜x＜120 |
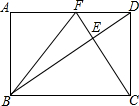在矩形ABCD中，DC=2$\sqrt{3}$，CF⊥BD分别交BD、AD于点E、F，连接BF．