题目内容
15.解方程组:$\left\{\begin{array}{l}{x:y=5:3}\\{x:z=7:2}\\{x-2y+3z=46}\end{array}\right.$.分析 方程组利用代入消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{x:y=5:3①}\\{x:z=7:2②}\\{x-2y+3z=46③}\end{array}\right.$
由①得y=$\frac{3}{5}$x④,
由②得z=$\frac{2}{7}$x⑤,
把y=$\frac{3}{5}$x,z=$\frac{2}{7}$x代入③得,x-$\frac{6}{5}$x+$\frac{6}{7}$x=46,
解得x=70,
把x=70代入④得y=42,
把x=70代入⑤得z=20,
所以这个方程组的解为$\left\{\begin{array}{l}{x=70}\\{y=42}\\{z=20}\end{array}\right.$.
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
11.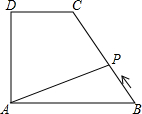 如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )
如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )
 如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )
如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )| A. | 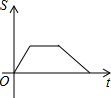 | B. | 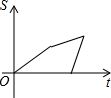 | C. | 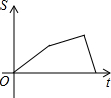 | D. | 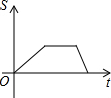 |
8.台湾是我国最大的岛屿,总面积为35989.76平方千米.用科学记数法应表示为(保留三个有效数字)( )平方千米.
| A. | 3.59×106 | B. | 3.60×106 | C. | 3.59×104 | D. | 3.60×104 |
9. 如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
 如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )| A. | $\frac{4}{25}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
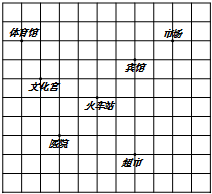 (1)如图,若以火车站为坐标原点,建立平面直角坐标系,超市的坐标为:(2,-3),则市场的坐标:(4,3),文化宫的坐标:(-3,1);
(1)如图,若以火车站为坐标原点,建立平面直角坐标系,超市的坐标为:(2,-3),则市场的坐标:(4,3),文化宫的坐标:(-3,1);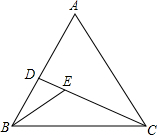 如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E.连接BE,∠BED=60°.若CE=6,△ACD的面积为$12\sqrt{3}$,则线段DB的长为4.
如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E.连接BE,∠BED=60°.若CE=6,△ACD的面积为$12\sqrt{3}$,则线段DB的长为4.