题目内容
18.若一个正多边形的一个内角等于135°,那么这个多边形是正八边形,内角和为1080°.分析 一个正多边形的每个内角都相等,根据内角与外角互为邻补角,因而就可以求出外角的度数.根据任何多边形的外角和都是360°,利用360°除以外角的度数就可以求出外角和中外角的个数,即多边形的边数,根据内角和公式即可求出内角和.
解答 解:∵内角与外角互为邻补角,
∴正多边形的一个外角是180°-135°=45°,
∵多边形外角和为360°,
∴360°÷45°=8,
则这个多边形是八边形.
∴内角和为:(8-2)×180°=1080°.
故答案为:八,1080.
点评 本题考查了多边形的内角与外角,解决本题的关键是由外角和求正多边形的边数.

练习册系列答案
相关题目
6.9的平方根是( )
| A. | ±3 | B. | 3 | C. | -33 | D. | $\sqrt{3}$ |
3.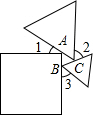 一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
 一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )| A. | 100° | B. | 120° | C. | 130° | D. | 180° |
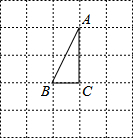 如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°.
如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°. 如图,△ABC中,AD是边BC的中线,S△ABD=24,则S△ACD=24.
如图,△ABC中,AD是边BC的中线,S△ABD=24,则S△ACD=24. 如图,△ABC是边长为$\sqrt{3}$的等边三角形,点P.Q分别是射线AB、BC上两个动点,且AP=CQ,PQ交AC与D,作PE丄AC于E,那么DE的长度为$\frac{1}{2}$$\sqrt{3}$.
如图,△ABC是边长为$\sqrt{3}$的等边三角形,点P.Q分别是射线AB、BC上两个动点,且AP=CQ,PQ交AC与D,作PE丄AC于E,那么DE的长度为$\frac{1}{2}$$\sqrt{3}$.