题目内容
12.已知一次函数图象经过点(-2,7),(2,-1)(1)求这个一次函数解析式;
(2)求出图象与两个坐标轴的交点坐标.
分析 (1)待定系数法求解可得;
(2)在函数解析式中,令x=0、y=0可分别求得图象与y轴和x轴的交点.
解答 解:(1)设该一次函数的解析式为y=kx+b,
根据题意,得:$\left\{\begin{array}{l}{-2k+b=7}\\{2k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=3}\end{array}\right.$,
∴这个一次函数解析式为y=-2x+3;
(2)在这个一次函数解析式y=-2x+3中,
当x=0时,y=3,
∴该函数图象与y轴交于点(0,3);
当y=0时,-2x+3=0,
解得:x=$\frac{3}{2}$,
∴该函数图象与x轴交于点($\frac{3}{2}$,0).
点评 本题主要考查待定系数法求一次函数解析式,待定系数法求一次函数解析式一般步骤是:
(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;
(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;
(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
2.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如表(单位:环):
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)已知甲六次成绩的方差S甲2=$\frac{2}{3}$,试计算乙六次测试成绩的方差;根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(2)已知甲六次成绩的方差S甲2=$\frac{2}{3}$,试计算乙六次测试成绩的方差;根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
20.$\frac{2•tan30°}{1-ta{n}^{2}30°}$的值等于( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{-\sqrt{3}}{3}$ |
7.一列数:0,1,2,3,6,7,14,15,30、这串数是由小明按照一定规则写下来的,他第一次写下“0,1”,第二次接着写“2,3”,第三次接着写“6,7”,第四次接着写“14,15”,就这样一直接着往下写,那么这串数接下来的三个数应该是下面的( )
| A. | 30,32,64 | B. | 31,62,63 | C. | 31,32,33 | D. | 31,45,46 |
17.已知2x2+y=1,x2-xy=2,则3x2+y(1-x)-1=( )
| A. | 4 | B. | -1 | C. | 3 | D. | 2 |

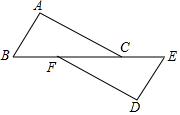 已知:如图,点B、F、C、E在一条直线上,∠B=∠E,∠ACB=∠DFE,且BF=EC.求证:△ABC≌△DEF.
已知:如图,点B、F、C、E在一条直线上,∠B=∠E,∠ACB=∠DFE,且BF=EC.求证:△ABC≌△DEF.