题目内容
1.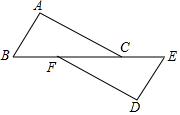 已知:如图,点B、F、C、E在一条直线上,∠B=∠E,∠ACB=∠DFE,且BF=EC.求证:△ABC≌△DEF.
已知:如图,点B、F、C、E在一条直线上,∠B=∠E,∠ACB=∠DFE,且BF=EC.求证:△ABC≌△DEF.
分析 首先求出BC=EF,进而利用全等三角形的判定定理ASA证明两个三角形全等.
解答 解:∵BF=EC
∴BF+CF=EC+CF,
∴BC=EF,
在△ABC和△DEF中,
∵$\left\{\begin{array}{l}{∠B=∠E}\\{BC=EF}\\{∠ACB=∠DFE}\end{array}\right.$
∴△ABC≌△DEF (ASA).
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.计算(-$\sqrt{5}$)2+($\sqrt{2}$)0-|$\sqrt{3}$-3|的结果是( )
| A. | 3+$\sqrt{3}$ | B. | 9-$\sqrt{3}$ | C. | -$\sqrt{5}$-2 | D. | $\sqrt{5}$-2 |
6.如果|a+2|+(b-1)2=0,那么代数式(a+b)2016的值是( )
| A. | -2011 | B. | 2011 | C. | -1 | D. | 1 |
13.某工艺厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.表是某周的生产情况(超产记为正、减产记为负):
(1)本周产量中最多的一天比最少的一天多生产多少个工艺品?
(2)请求出该工艺厂在本周实际生产工艺品的数量;
(3)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,若生产不足则每少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减(单位:个) | +1 | -2 | -7 | +12 | -15 | +10 | -9 |
(2)请求出该工艺厂在本周实际生产工艺品的数量;
(3)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,若生产不足则每少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
10.若方程(m-2)x2-3x-2=0是关于x的一元二次方程,则m的取值范围是( )
| A. | m>2 | B. | m≠2 | C. | m>0 | D. | m≠0 |
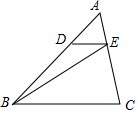 如图,△ABC中,D、E分别是边AB、AC 上的点,且∠DEB=∠EBC.
如图,△ABC中,D、E分别是边AB、AC 上的点,且∠DEB=∠EBC.