题目内容
9. 如图,将一张边长为m的正方形纸片,第一次剪成四个大小形状一样的小正方形,然后再将其中的一个小正方形按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下表.
如图,将一张边长为m的正方形纸片,第一次剪成四个大小形状一样的小正方形,然后再将其中的一个小正方形按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下表.(1)观察图形,填写下表:
| 剪的次数 | 1 | 2 | 3 |
| 正方形个数 | 4 | 7 | 10 |
| 最小正方形边长 | $\frac{1}{2}$m | $\frac{1}{4}$m | $\frac{1}{8}$m |
分析 (1)根据图形即可得出答案;
(2)由表格的出每多剪一次多3个小正方形,且其边长为原正方形边长的$\frac{1}{{2}^{n}}$倍,据此可得.
解答 解:(1)
| 剪的次数 | 1 | 2 | 3 |
| 正方形个数 | 4 | 7 | 10 |
| 最小正方形边长 | $\frac{1}{2}$m | $\frac{1}{4}$m | $\frac{1}{8}$m |
故答案为:3n+1,$\frac{m}{{2}^{n}}$.
点评 本题主要考查图形变化类,根据题意得出每多剪一次多3个小正方形,且其边长为原正方形边长的$\frac{1}{{2}^{n}}$倍是解题的关键.

练习册系列答案
相关题目
18.已知点P(1-2a,a+3)在第二象限,则a的取值范围是( )
| A. | a<-3 | B. | a>$\frac{1}{2}$ | C. | -$\frac{1}{2}$<a<3 | D. | -3<a<$\frac{1}{2}$ |
19.二次函数y=x2-4x-4的顶点坐标为( )
| A. | (2,-8) | B. | (2,8) | C. | (-2,8) | D. | (-2,-8) |
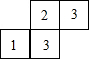 一个几何体由几个大小相同的小立方体搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.
一个几何体由几个大小相同的小立方体搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.