题目内容
16. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BC=2AC,则cot∠BCD=$\frac{1}{2}$.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BC=2AC,则cot∠BCD=$\frac{1}{2}$.
分析 先证明Rt△ABC∽Rt△BDC,从而证明∠A=∠BCD,再根据锐角三角函数的定义求解即可.
解答 解:∵∠ACB=90°,CD⊥AB,
∴∠ACB=∠CDB=90°,
在Rt△ABC和Rt△BDC中,
∠B=∠B,∠ACB=∠BDC=90°,
∴Rt△ABC∽Rt△BDC,
∴∠A=∠BCD,
∴cot∠BCD=$\frac{AC}{BC}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查了勾股定理和三角函数的定义.解题时牢记定理和定义是关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
4.下列式子中不正确的是( )
| A. | sin60°=$\frac{\sqrt{3}}{2}$ | B. | tan30°•tan60°=1 | ||
| C. | sin230°+cos230°=1 | D. | sin$\frac{1}{2}$=30° |
1.若x2+mxy+4y2是完全平方式,则常数m的值为( )
| A. | 4 | B. | -4 | C. | ±4 | D. | 以上结果都不对 |
5.2014年西安城墙国际马拉松赛已于11月1日上午9:00在西安城墙南门上举行,所有参赛选手要跑完全程,约为13.7千米.那么13.7千米用科学记数法可表示为( )
| A. | 1.37×103米 | B. | 13.7×103米 | C. | 1.37×104米 | D. | 13.7×102米 |
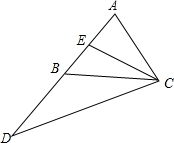 如图,在△ABC中,AC=AB,CE是AB边上的中线,延长AB至D,使BD=AB,问CE与CD有何数量关系?请说明理由.
如图,在△ABC中,AC=AB,CE是AB边上的中线,延长AB至D,使BD=AB,问CE与CD有何数量关系?请说明理由.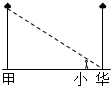 如图,甲、乙两盏路灯底部间的距离是25米,一天晚上,当小华走到距路灯乙底部4米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.6米,那么路灯甲的高为10米.
如图,甲、乙两盏路灯底部间的距离是25米,一天晚上,当小华走到距路灯乙底部4米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.6米,那么路灯甲的高为10米. 如图,在数轴上有O,A,B,C,D五点,根据图中各点所表示的数,判断$\sqrt{18}$在数轴上的位置会落在线段BC上.
如图,在数轴上有O,A,B,C,D五点,根据图中各点所表示的数,判断$\sqrt{18}$在数轴上的位置会落在线段BC上.