题目内容
17．
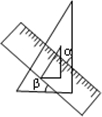将一个直角三角板和一把直尺如图放置，如果∠α=53°，则∠β=37°．
分析 首先过点C作CH∥DE交AB于H，即可得CH∥DE∥FG，然后利用两直线平行，同位角相等与余角的性质，即可求得∠β的度数．
解答 
解：如图，根据题意得：∠ACB=90°，DE∥FG，
过点C作CH∥DE交AB于H，
∴CH∥DE∥FG，
∴∠BCH=∠α=53°，
∴∠HCA=90°-∠BCH=37°，
∴∠β=∠HCA=37°．
故答案为：37．
点评 此题考查了平行线的性质．此题难度不大，解题的关键是准确作出辅助线，掌握两直线平行，同位角相等定理的应用．
练习册系列答案
全程金卷系列答案
相关题目
7．分式$\frac{{{x^2}-9}}{x+3}$的值为0，则x的值为（ ）
| A． | -3 | B． | 3 | C． | 0 | D． | ±3 |
8．
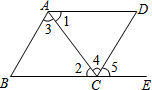如图，下列条件中：①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5，能判定AB∥CD的条件为（ ）
如图，下列条件中：①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5，能判定AB∥CD的条件为（ ）| A． | ①②③④ | B． | ①②④ | C． | ①③④ | D． | ①②③ |
12．
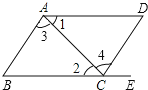如图，给出下列条件：①∠1=∠2；②∠3=∠4；③AD∥BE，且∠D=∠B；其中，能推出AB∥DC的条件为（ ）
如图，给出下列条件：①∠1=∠2；②∠3=∠4；③AD∥BE，且∠D=∠B；其中，能推出AB∥DC的条件为（ ）| A． | ①② | B． | ①③ | C． | ②③ | D． | 以上都错 |
9．根据下列条件，能判断出一个四边形是平行四边形的是（ ）
| A． | 一组对边相等 | B． | 两条对角线互相垂直 | ||
| C． | 一组对边平行 | D． | 两条对角线互相平分 |
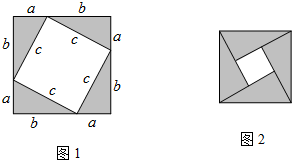阅读下面的材料