��Ŀ����
7��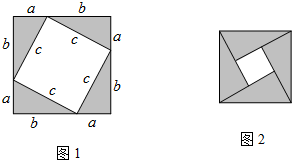 �Ķ�����IJ���
�Ķ�����IJ������ɶ������ض��������֤�����ֶ����������ǽ̲��н��ܵ�һ��ƴͼ֤�����ɶ����ķ����������ĸ�ȫ�ȵ�ֱ�������Σ������ǵ�����ֱ�DZ߷ֱ�Ϊa��b��б��Ϊc��Ȼ��ͼ1�ķ��������ǰڳ������Σ�
��ͼ1���Եõ���a+b��2=4��$\frac{1}{2}ab+{c^2}$��
��������a2+2ab+b2=2ab+c2��
����a2+b2=c2��
�����ͼ1�е��ĸ�ȫ�ȵ�ֱ�������ΰڳ�ͼ2��ʾ�������Σ���
���������֤�����ɶ����ķ���������������գ�
��ͼ2���Եõ�$4��\frac{1}{2}ab+��b-a{��^2}={c^2}$��
��������2ab+b2-2ab+a2=c2��
����a2+b2=c2��
���� ͨ��������������ε����֮����ȵĹ�ϵ����֤�����ɶ�����
���  ֤������S��������=c2��S��������=4S��+SС������=4��$\frac{1}{2}$ab+��b-a��2��
֤������S��������=c2��S��������=4S��+SС������=4��$\frac{1}{2}$ab+��b-a��2��
��c2=4��$\frac{1}{2}$ab+��b-a��2��
��������
2ab+b2-2ab+a2=c2��
��c2=a2+b2��
�ʴ��ǣ�$4��\frac{1}{2}ab+��b-a{��^2}={c^2}$��2ab+b2-2ab+a2=c2��a2+b2=c2��
���� ���⿼������ͼ������Ĺ�ϵ֤�����ɶ���������ؼ������������κ������α߳��Ĺ�ϵ�������ͼ�Σ�

��ϰ��ϵ�д�
�����Ŀ
12����8000�ÿ�ѧ��������ʾ�ǣ�������
| A�� | 80��102 | B�� | 8��103 | C�� | 0.8��104 | D�� | 8��104 |
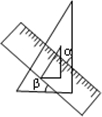 ��һ��ֱ�����ǰ��һ��ֱ����ͼ���ã�����Ϧ�=53�㣬��Ϧ�=37�㣮
��һ��ֱ�����ǰ��һ��ֱ����ͼ���ã�����Ϧ�=53�㣬��Ϧ�=37�㣮