题目内容
6.求同时满足以下条件的a、b.(1)a2+b2=144
(2)y=3x2+15与y=ax+b图象有公共点.
分析 由a2+b2=144,可得a2=144-b2.由y=3x2+15与y=ax+b图象有公共点,得出一元二次方程3x2-ax+15-b=0有实数根,那么△=(-a)2-4×3(15-b)≥0,将a2=144-b2代入,整理得出-(b-6)2≥0,根据非负数的性质得到b=6,进而求出a的值.
解答 解:∵a2+b2=144,
∴a2=144-b2 .
∵y=3x2+15与y=ax+b图象有公共点,
∴一元二次方程3x2-ax+15-b=0有实数根,
∴△=(-a)2-4×3(15-b)≥0,
∴a2-180+12b≥0,
将a2=144-b2代入,得144-b2-180+12b≥0,
∴-(b-6)2≥0,
∵-(b-6)2≤0,
∴b=6,
∴a2=144-62 =108,
∴a=±6$\sqrt{3}$.
点评 本题考查了二次函数与一次函数的交点,二次函数与一元二次方程的关系,非负数的性质,根据y=3x2+15与y=ax+b图象有公共点,得出一元二次方程3x2-ax+15-b=0有实数根是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
16.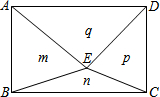 如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:
如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:
①m+n=q+p;
②m+p=n+q;
③若m=n,则E点一定是AC与BD的交点;
④若m=n,则E点一定在BD上.
其中正确结论的序号是( )
 如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:
如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:①m+n=q+p;
②m+p=n+q;
③若m=n,则E点一定是AC与BD的交点;
④若m=n,则E点一定在BD上.
其中正确结论的序号是( )
| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ②③④ |
14. 随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速超过60千米即为违章,则这次检测到的违章车辆共有76辆.
 随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):| 时速数据段 | 频数 | 频率 |
| 30-40 | 10 | 0.05 |
| 40-50 | 36 | 0.18 |
| 50-60 | 78 | 0.39 |
| 60-70 | 56 | 0.28 |
| 70-80 | 20 | 0.10 |
| 总计 | 200 | 1 |
(2)补全频数分布直方图;
(3)如果汽车时速超过60千米即为违章,则这次检测到的违章车辆共有76辆.
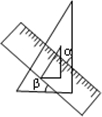 将一个直角三角板和一把直尺如图放置,如果∠α=53°,则∠β=37°.
将一个直角三角板和一把直尺如图放置,如果∠α=53°,则∠β=37°.