题目内容
8．
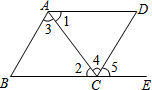如图，下列条件中：①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5，能判定AB∥CD的条件为（ ）| A． | ①②③④ | B． | ①②④ | C． | ①③④ | D． | ①②③ |
分析 根据平行线的判定定理求解，即可求得答案．
解答 解：①∵∠B+∠BCD=180°，
∴AB∥CD；
②∵∠1=∠2，
∴AD∥BC；
③∵∠3=∠4，
∴AB∥CD；
④∵∠B=∠5，
∴AB∥CD；
∴能得到AB∥CD的条件是①③④．
故选C．
点评 此题主要考查了平行线的判定，关键是掌握判定定理：同位角相等，两直线平行．内错角相等，两直线平行．同旁内角互补，两直线平行．
练习册系列答案
名校课堂系列答案
相关题目
如图，△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．
16．
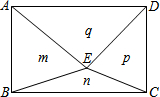如图，E是矩形ABCD内的一个动点，连接EA、EB、EC、ED，得到△EAB、△EBC、△ECD、△EDA，设它们的面积分别是m、n、p、q，给出如下结论：
①m+n=q+p；
②m+p=n+q；
③若m=n，则E点一定是AC与BD的交点；
④若m=n，则E点一定在BD上．
其中正确结论的序号是（ ）
如图，E是矩形ABCD内的一个动点，连接EA、EB、EC、ED，得到△EAB、△EBC、△ECD、△EDA，设它们的面积分别是m、n、p、q，给出如下结论：①m+n=q+p；
②m+p=n+q；
③若m=n，则E点一定是AC与BD的交点；
④若m=n，则E点一定在BD上．
其中正确结论的序号是（ ）
| A． | ①③ | B． | ②④ | C． | ①②③ | D． | ②③④ |
20．分式$\frac{m}{m+n}$，$\frac{-mn}{{{{（m+n）}^2}}}$，$\frac{n}{m-n}$的最简公分母是（ ）
| A． | （m+n）2（m-n） | B． | （m+n）3（m-n） | C． | （m+n）（m-n） | D． | （m2-n2）2 |
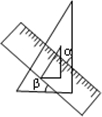将一个直角三角板和一把直尺如图放置，如果∠α=53°，则∠β=37°．