题目内容
3. 如图所示,已知AC=BD,CE=DF,AF=BE,求证:AC∥BD,CE∥DF.
如图所示,已知AC=BD,CE=DF,AF=BE,求证:AC∥BD,CE∥DF.
分析 易证△ACE≌BDF,则∠A=∠B,∠AEC=∠BFD,根据等角的补角相等得到∠CEF=∠DFE,于是AC∥BD,CE∥DF.
解答 证明:∵AF=BE,
∴AF-EF=BE-EF,
∴AE=BF,
在△ACE和△BDF中,
$\left\{\begin{array}{l}{AE=BF}\\{CE=DF}\\{AC=BD}\end{array}\right.$,
∴△ACE≌BDF(SSS),
∴∠A=∠B,∠AEC=∠BFD,
∴∠CEF=∠DFE,
∴AC∥BD,CE∥DF.
点评 此题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.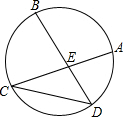 如图,弦AC、BD相交于点E,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,若∠AED=80°,则∠ACD的度数为( )
如图,弦AC、BD相交于点E,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,若∠AED=80°,则∠ACD的度数为( )
 如图,弦AC、BD相交于点E,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,若∠AED=80°,则∠ACD的度数为( )
如图,弦AC、BD相交于点E,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,若∠AED=80°,则∠ACD的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 15° |
10.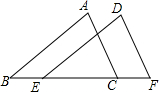 如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是( )
如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是( )
 如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是( )
如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是( )| A. | AB=DE | B. | ∠A=∠D | C. | AC∥DF | D. | AC=DF |
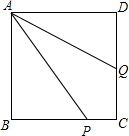 ABCD是正方形,P为BC上任意一点,∠PAD的平分线交CD于Q,求证:DQ=AP-BP.
ABCD是正方形,P为BC上任意一点,∠PAD的平分线交CD于Q,求证:DQ=AP-BP.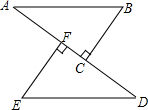 如图,AB=DE,BC⊥AD,EF⊥AD,垂足分别为C、F,且AF=DC,求证:AB∥DE.
如图,AB=DE,BC⊥AD,EF⊥AD,垂足分别为C、F,且AF=DC,求证:AB∥DE. 有理数a,b在数轴上如图,用“<”把b+a,b-a,a-b,-a-b按从小到大的顺序连接起来.
有理数a,b在数轴上如图,用“<”把b+a,b-a,a-b,-a-b按从小到大的顺序连接起来. 如图,已知数轴上两个点A,B分别互为相反数的两个数a,b,且A,B两点间距离为4,求a,b两数,它们的关系用等式怎样表示?
如图,已知数轴上两个点A,B分别互为相反数的两个数a,b,且A,B两点间距离为4,求a,b两数,它们的关系用等式怎样表示?