题目内容
18.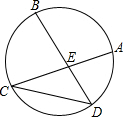 如图,弦AC、BD相交于点E,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,若∠AED=80°,则∠ACD的度数为( )
如图,弦AC、BD相交于点E,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,若∠AED=80°,则∠ACD的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 15° |
分析 首先设$\widehat{AB}$的度数为m,$\widehat{AD}$的度数为n,由圆心角、弧、弦的关系得出$\widehat{BC}$、$\widehat{CD}$的度数都为m,得出3m+n=360°,由圆周角定理和三角形外角的性质推知∠C+∠D=$\frac{1}{2}$m+$\frac{1}{2}$n=80°,组成方程组即可求得$\widehat{AD}$的度数,进而求得∠ACD的度数.
解答 解:如图,设$\widehat{AB}$的度数为m,$\widehat{AD}$的度数为n,
∵$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,
∴$\widehat{BC}$、$\widehat{CD}$的度数都为m,
∴3m+n=360°①
∵∠AED=80°,
∴∠C+∠D=80°,
∴$\frac{1}{2}$m+$\frac{1}{2}$n=80°②,
由①②组成$\left\{\begin{array}{l}{3m+n=360°}\\{\frac{1}{2}m+\frac{1}{2}n=80°}\end{array}\right.$,
解得m=100°,n=60°
∴$∠ACD=\frac{1}{2}n$=30°.
故选C.
点评 本题考查了圆周角定理,圆心角、弧、弦的关系,三角形外角的性质等,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
5.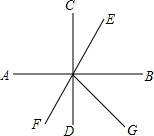 如图,直线AB、CD、EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°.则∠BOG的度数为( )
如图,直线AB、CD、EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°.则∠BOG的度数为( )
 如图,直线AB、CD、EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°.则∠BOG的度数为( )
如图,直线AB、CD、EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°.则∠BOG的度数为( )| A. | 90° | B. | 60° | C. | 30° | D. | 无法确定 |
 如图,在△ABC中,BD是∠ABC的平分线,DE∥BC交AB于E,EF∥AC交BC于F,猜想BE与CF的数量关系,并说明理由.
如图,在△ABC中,BD是∠ABC的平分线,DE∥BC交AB于E,EF∥AC交BC于F,猜想BE与CF的数量关系,并说明理由. 如图所示,已知AC=BD,CE=DF,AF=BE,求证:AC∥BD,CE∥DF.
如图所示,已知AC=BD,CE=DF,AF=BE,求证:AC∥BD,CE∥DF.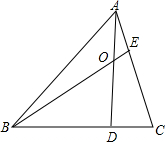 如图,已知在△ABC中,BD:DC=3:1,AE:CE=1:2,S△ABC=48,求四边形ODCE的面积.
如图,已知在△ABC中,BD:DC=3:1,AE:CE=1:2,S△ABC=48,求四边形ODCE的面积.