题目内容
10.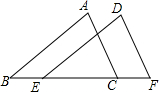 如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是( )
如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是( )| A. | AB=DE | B. | ∠A=∠D | C. | AC∥DF | D. | AC=DF |
分析 首先根据等式的性质可得BC=EF,再根据平行线的性质可得∠A=∠DEF,再分别添加四个选项中的条件,结合全等三角形的判定定理进行分析即可.
解答 解:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
∵AB∥DE,
∴∠A=∠DEF,
A、添加AB=DE,可利用SAS判定△ABC≌△DEF,故此选项不合题意;
B、添加∠A=∠D,可利用AAS判定△ABC≌△DEF,故此选项不合题意;
C、添加AC∥DF,可得∠ACB=∠F,可利用ASA判定△ABC≌△DEF,故此选项不合题意;
D、添加AC=DF,不能判定△ABC≌△DEF,故此选项符合题意;
故选:D.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.圆的面积为$\frac{9}{4}$π,则60°的圆心角所对的弧长是( )
| A. | $\frac{3}{2}$ | B. | $\frac{π}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{π}{4}$ |
5.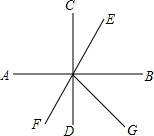 如图,直线AB、CD、EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°.则∠BOG的度数为( )
如图,直线AB、CD、EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°.则∠BOG的度数为( )
 如图,直线AB、CD、EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°.则∠BOG的度数为( )
如图,直线AB、CD、EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°.则∠BOG的度数为( )| A. | 90° | B. | 60° | C. | 30° | D. | 无法确定 |
15.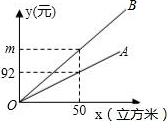 某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;
某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;
方案二如表所示,每月的每立方米用水价格由该月的用水量决定,其第一、二、三阶的用水价格之比为1:1.5:2(精确到0.01元)
(1)现行的用水量是每立方米1.84元,第三阶的用水价格a=5.22;
(2)求图中m的值和射线OB所对应的函数关系式;
(3)若小明家某月的用水量是a(立方米),请分别写出所提的两种方案下该月的水费b(元)【用含a的代数式表示】
 某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;
某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;方案二如表所示,每月的每立方米用水价格由该月的用水量决定,其第一、二、三阶的用水价格之比为1:1.5:2(精确到0.01元)
| 阶数 | 用水量(立方米) | 用水价格(元/立方米) |
| 第一阶 | 0~15(含15)的部分 | 2.61 |
| 第二阶 | 15~25(含25)的部分 | 3.92 |
| 第三阶 | 25以上的得分 | n |
(2)求图中m的值和射线OB所对应的函数关系式;
(3)若小明家某月的用水量是a(立方米),请分别写出所提的两种方案下该月的水费b(元)【用含a的代数式表示】
20.-22的相反数是( )
| A. | -4 | B. | 2 | C. | -2 | D. | 4 |
 如图所示,已知AC=BD,CE=DF,AF=BE,求证:AC∥BD,CE∥DF.
如图所示,已知AC=BD,CE=DF,AF=BE,求证:AC∥BD,CE∥DF.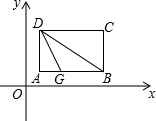 如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.
如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.