题目内容
海安是全国著名的茧丝纸之乡,某丝绸公司承担茧丝丝绸产品的加工出口任务,现有一批产品需要装入某一规格的纸箱,供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由丝绸公司租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.公司需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱x个,请分别用x的代数式表示:从纸箱厂购买纸箱的费用 元;丝绸公司自己加工制作纸箱的费用 元.
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由丝绸公司租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.公司需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱x个,请分别用x的代数式表示:从纸箱厂购买纸箱的费用
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
考点:一次函数的应用
专题:
分析:(1)根据价格乘以数量求得从纸箱厂购买纸箱的费用;利用价格乘以数量然后加上机器的费用16000元就是自己加工制作纸箱的费用;
(2)比较(1)中的两个代数式的大小从而确定.
(2)比较(1)中的两个代数式的大小从而确定.
解答:解:(1)从纸箱厂购买纸箱的费用4x元;丝绸公司自己加工制作纸箱的费用16000+2.4x元.
故答案是:4x,16000+2.4x;
(2)当4x>16000+2.4x时,x>10000,选择方案二合适;
当4x=16000+2.4x,解得x=10000,此时利用两个方案相同;
当4x<16000+2.4x,即x<10000时,选择方案一比较合适.
故答案是:4x,16000+2.4x;
(2)当4x>16000+2.4x时,x>10000,选择方案二合适;
当4x=16000+2.4x,解得x=10000,此时利用两个方案相同;
当4x<16000+2.4x,即x<10000时,选择方案一比较合适.
点评:本题考查了一次函数的应用,利用一次函数性质解决生活中的实际问题.需要讨论x的取值.

练习册系列答案
相关题目
 如图,已知∠1+∠2=180°,∠C=∠D,则∠A=∠F吗?为什么?
如图,已知∠1+∠2=180°,∠C=∠D,则∠A=∠F吗?为什么?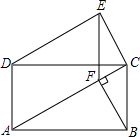 如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°,过点B作BF⊥AC于点F,连结EF,求证:
如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°,过点B作BF⊥AC于点F,连结EF,求证: