题目内容
14. 从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.
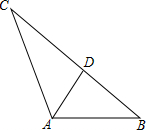
从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.(1)如图,在△ABC中,AD为角平分线,∠B=50°,∠C=30°,求证:AD为△ABC的优美线.
(2)在△ABC中,∠B=46°,AD是△ABC的优美线,且△ABD是以AB为腰的等腰三角形,求∠BAC的度数.
(3)在△ABC中,AB=4,AC=2,AD是△ABC的优美线,且△ABD是等腰三角形,求优美线AD的长.
分析 (1)根据三角形的优美线的定义,只要证明△ABD是等腰三角形,△CAD∽△CBA即可解决问题.
(2)如图2中,分两种情形讨论求解①若AB=AD,△CAD∽△CBA,则∠B=∠ADB=∠CAD,则AC∥BC,这与△ABC这个条件矛盾;②若AB=BD,△CAD∽△CBA;
(3)如图3中,分三种情形讨论①若AD=BD,△CAD∽△CBA,则$\frac{AD}{AB}$=$\frac{CD}{AC}$=$\frac{AC}{BC}$,设BD=AD=x,CD=y,可得$\frac{x}{4}$=$\frac{y}{2}$=$\frac{2}{x+y}$,解方程即可;②若AB=AD=4,由$\frac{AD}{AB}$=$\frac{CD}{AC}$=$\frac{AC}{BC}$,设BD=AD=x,CD=y,可得$\frac{x}{4}$=$\frac{y}{2}$=$\frac{2}{4+y}$,解方程即可;③若AB=AD,显然不可能;
解答 解:(1)如图1中,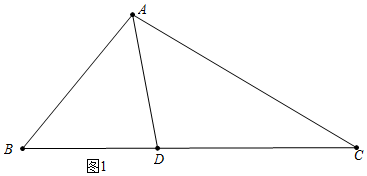
∵∠B=50°,∠C=30°,
∴∠BAC=180°-∠B-∠C=100°,
∵AD平分∠BAC,
∴∠BAD=∠DAC=50°,
∴∠B=∠BAD=50°,
∴DB=DA,
∴△ABD是等腰三角形,
∵∠C=∠C,∠DAC=∠B=50°,
∴△CAD∽△CBA,
∴线段AD是△ABC的优美线.
(2)如图2中,
若AB=AD,△CAD∽△CBA,则∠B=∠ADB=∠CAD,则AC∥BC,这与△ABC这个条件矛盾;
若AB=BD,△CAD∽△CBA,∠B=46°,
∴∠BAD=∠BDA=67°,
∵∠CAD=∠B=46°,
∴∠BAC=67°+46°=113°.
(3)如图3中,
若AD=BD,△CAD∽△CBA,
则$\frac{AD}{AB}$=$\frac{CD}{AC}$=$\frac{AC}{BC}$,设BD=AD=x,CD=y,
∴$\frac{x}{4}$=$\frac{y}{2}$=$\frac{2}{x+y}$,
解得x=$\frac{4\sqrt{3}}{3}$,y=$\frac{2\sqrt{3}}{3}$,
∴AD=$\frac{4\sqrt{3}}{3}$.
若AB=AD=4,由$\frac{AD}{AB}$=$\frac{CD}{AC}$=$\frac{AC}{BC}$,设BD=AD=x,CD=y,
可得$\frac{x}{4}$=$\frac{y}{2}$=$\frac{2}{4+y}$,解得y=-2+2$\sqrt{2}$,x=4$\sqrt{2}$-4(负根已经舍弃),
∴AD=4$\sqrt{2}$-4.
若AB=AD,显然不可能,
综上所述,AD=$\frac{4\sqrt{3}}{3}$或4$\sqrt{2}$-4.
点评 本题考查相似三角形综合题、等腰三角形的判定和性质、相似三角形的判定和性质一元二次方程等知识,解题的关键是理解题意,学会用方程的思想思考问题,属于中考压轴题.

| A. | 18 | B. | 8 | C. | 7 | D. | 11 |
 如图,把边长为4cm的正方形ABCD先向右平移1cm再向上平移1cm得到正方形EFGH,则阴影部分的面积为9cm2.
如图,把边长为4cm的正方形ABCD先向右平移1cm再向上平移1cm得到正方形EFGH,则阴影部分的面积为9cm2.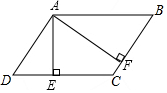 如图,在平行四边形ABCD中,AE⊥CD,垂足为E,AF⊥BC,垂足为F,AD=4,BF=3,∠EAF=60°,设$\overrightarrow{AB}$=$\overrightarrow{a}$,如果向量$\overrightarrow{CE}$=k$\overrightarrow{a}$(k≠0),那么k的值是-$\frac{2}{3}$.
如图,在平行四边形ABCD中,AE⊥CD,垂足为E,AF⊥BC,垂足为F,AD=4,BF=3,∠EAF=60°,设$\overrightarrow{AB}$=$\overrightarrow{a}$,如果向量$\overrightarrow{CE}$=k$\overrightarrow{a}$(k≠0),那么k的值是-$\frac{2}{3}$.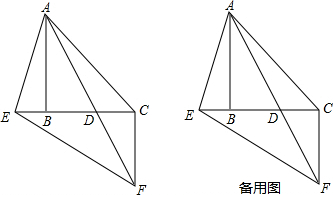
 如图,正方形OABC的边长为2,点A在x轴上,点C在y轴上,函数y=-$\frac{2}{3}$x2+bx+c的图象经过点B和点C,直线CA交抛物线于点P,PQ⊥x轴于点Q.
如图,正方形OABC的边长为2,点A在x轴上,点C在y轴上,函数y=-$\frac{2}{3}$x2+bx+c的图象经过点B和点C,直线CA交抛物线于点P,PQ⊥x轴于点Q.