题目内容
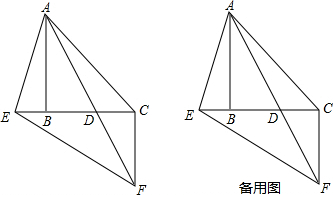
3.如图,△ABC为等腰直角三角形,∠ABC=90°,点D在线段BC上,点E在CB的延长线上,∠EAD=45°.(1)求证:△EAD∽△ECA;
(2)若∠AED=75°,求证:DE=2CD;
(3)过C作CF⊥BC交AD延长线于F,连EF,若P、Q两点分别同时从B点出发,以相同的速度沿B→E→F和B→C→F运动,问点P、点Q谁先到达,并说明理由.
分析 (1)根据两角对应相等两三角形相似即可证明.
(2)如图2中,作AM⊥FC交FC的延长线于M,在MC上截取MN=EB,连接AN.只要证明△ABE≌△AMN,推出∠EAB=∠MAN,AE=AN,推出△FAE≌△FAN,推出∠AFE=∠AFN=30°即可解决问题.
(3)点P与点Q同时到达目的地.只要证明BE+EF=BC+CF即可.
解答 (1)证明:如图1中,
∵BA=BC,∠ABC=90°,
∴∠BAC=∠ACB=45°,∵∠EAD=45°,
∴∠EAD=∠ACE,∵∠AED=∠CEA,
∴△EAD∽△ECA;
(2)证明:如图2中,作AM⊥FC交FC的延长线于M,在MC上截取MN=EB,连接AN.
∵CF⊥CB,
∴∠ABC=∠BCM=∠M=90°,
∴四边形ABCM是矩形,
∵BA=BC,
∴四边形ABCM是正方形,
∵AB=AM,∠ABE=∠M,EB=MN,
∴△ABE≌△AMN,
∴∠EAB=∠MAN,AE=AN
∵∠EAD=45°,
∴∠EAB+∠BAD=∠MAN+∠BAD=45°,
∵∠MAB=90°,
∴∠FAN=45°=∠FAE,∵FA=FA,AE=AN,
∴△FAE≌△FAN,
∴∠AFE=∠AFN,
∵∠AED=75°,∠EAD=45°,
∴∠ADE=∠FDC=60°,∵∠DCF=90°,
∴∠AFE=∠AFC=30°,
∴DF=2CD,
∵∠FDC=∠DEF+∠DFE=60°,
∴∠DEF=∠DFE=30°,
∴DE=DF=2CD,
即DE=2CD;
(3)解:结论:点P与点Q同时到达目的地.理由如下:
如图2中,∵△FAE≌△FAN,
∴EF=BN,∵BE=MN,
∴EB+EF=MN+FN=FM,BC+CF=CM+CF=FM,
∴BE+EF=BC+CF,
∴若P、Q两点分别同时从B点出发,以相同的速度沿B→E→F和B→C→F运动,点P与点Q同时到达目的地.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质.正方形的判定和性质、直角三角形30度角性质、等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案 如图,直线a∥b,直线c与直线a,b都相交,若∠1=55°,则∠2等于( )
如图,直线a∥b,直线c与直线a,b都相交,若∠1=55°,则∠2等于( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
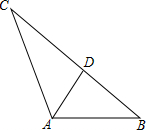 从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.
从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.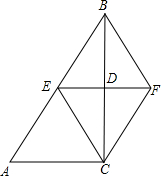 如图在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,请你添加一个条件AC=BC,使四边形BECF是正方形.
如图在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,请你添加一个条件AC=BC,使四边形BECF是正方形.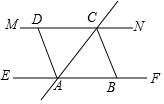 已知EF∥MN,直线AC交EF、MN于点A、C,作∠ACN的角平分线于点B,作∠CAE的角平分线交MN于点D.
已知EF∥MN,直线AC交EF、MN于点A、C,作∠ACN的角平分线于点B,作∠CAE的角平分线交MN于点D.