题目内容
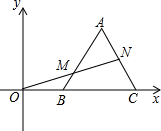 如图,平面直角坐标系内,正三角形ABC的顶点B,C的坐标分别为(2,0),(6,0),过坐标原点O的一条直线分别与边AB,AC交于点M,N,若OM=MN,则点M的坐标为
如图,平面直角坐标系内,正三角形ABC的顶点B,C的坐标分别为(2,0),(6,0),过坐标原点O的一条直线分别与边AB,AC交于点M,N,若OM=MN,则点M的坐标为考点:等边三角形的性质,坐标与图形性质
专题:
分析:从OM=MN结合点B和点C的坐标求得AN等于2,并结合等边三角形ABC点B和点C的坐标,从而求得点M坐标.
解答: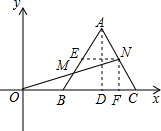 解:∵B(2,0),C(6,0),
解:∵B(2,0),C(6,0),
∴OB=2,OC=6,
∴BC=4,
过点N作EN∥OC交AB于E,过点A作AD⊥BC于D,NF⊥BC于F,
∴∠ENM=∠BOM,
在△ENM与△BOM中,
∵
,
∴△ENM≌△BOM(ASA),
∴EN=OB=2,
∵△ABC是正三角形,
∴AD=2
,BD=
BC=2,
∴OD=4,
∴A(4,2
),
∴△AEN也是正三角形,
∴AN=EN=2,
∴AN=CN,
∴N(5,
),
∴M(
,
).
故答案为:(
,
).
 解:∵B(2,0),C(6,0),
解:∵B(2,0),C(6,0),∴OB=2,OC=6,
∴BC=4,
过点N作EN∥OC交AB于E,过点A作AD⊥BC于D,NF⊥BC于F,
∴∠ENM=∠BOM,
在△ENM与△BOM中,
∵
|
∴△ENM≌△BOM(ASA),
∴EN=OB=2,
∵△ABC是正三角形,
∴AD=2
| 3 |
| 1 |
| 2 |
∴OD=4,
∴A(4,2
| 3 |
∴△AEN也是正三角形,
∴AN=EN=2,
∴AN=CN,
∴N(5,
| 3 |
∴M(
| 5 |
| 2 |
| ||
| 2 |
故答案为:(
| 5 |
| 2 |
| ||
| 2 |
点评:本题考查的是等边三角形的性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
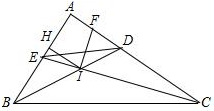 如图,△ABC中,∠A=90°,角平分线BD、CE交于点I,IF⊥CE交CA于F,IH⊥AB于H,下列结论:①∠DIF=45°;②CF+BE=BC;③AE+AF=2AH;④S四边形△BEDC=2S△IBC,其中正确结论的个数为( )
如图,△ABC中,∠A=90°,角平分线BD、CE交于点I,IF⊥CE交CA于F,IH⊥AB于H,下列结论:①∠DIF=45°;②CF+BE=BC;③AE+AF=2AH;④S四边形△BEDC=2S△IBC,其中正确结论的个数为( )| A、1个 | B、2个 | C、3个 | D、4个 |
若m>0,n<0,则一定有( )
| A、m-|n|>0 |
| B、m+n>0 |
| C、m2+n3>0 |
| D、n2+m3>0 |
计算(-
)2的结果是( )
| 3x |
| x+y |
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知:如图,A、C、F、D在同一直线上,AF=CD,AB=DE,BC=EF,求证:∠B=∠E.
已知:如图,A、C、F、D在同一直线上,AF=CD,AB=DE,BC=EF,求证:∠B=∠E.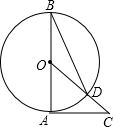 已知,如图所示,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.求∠ABD的度数.
已知,如图所示,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.求∠ABD的度数. 如图,在等腰△ABC中,∠A=100°,BD是∠ABC的平分线.求证:BD+AD=BC.
如图,在等腰△ABC中,∠A=100°,BD是∠ABC的平分线.求证:BD+AD=BC.